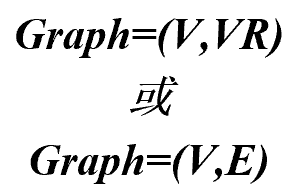图论

基本概念

由顶点集合V和一个描述顶点之间关系—-边的集合VR(或E)组成。

图的定义

V：顶点(数据元素)的有穷非空集合。

VR(或E)：弧(关系)的有穷集合。

相关术语

顶点 数据元素所构成的结点。

有向图 弧的顶点偶对是有序的。
对弧<vi, vj>而言，vi是弧尾/初始点；vj是弧头/终端点。

无向图 弧的顶点偶对是无序的。
(vi,vj)和(vj, vi)代表同一条边(i!=j)。

(无向)完全图 每个顶点与其余顶点都有边的无向图。
顶点数为n时，边数 e=n(n-1)/2

有向完全图 每个顶点与其余顶点都有弧的有向图。
顶点数为n时，弧数 e=n(n-1)

稀疏图 有很少边或弧的图。（e<nlogn）

稠密图 有较多边或弧的图。

权 图中的边或弧具有一定的大小的概念。

网 边/弧带权的图。

邻接 有边/弧相连的两个顶点之间的关系。
存在(vi,vj)，则称vi和vj互为邻接点；

关联(依附) 边/弧与顶点之间的关系。
存在(vi,vj)/ <vi, vj>， 则称该边/弧关联于vi和vj

顶点的度 与该顶点相关联的边的数目，记为D(v)。
入度ID(v)：有向图中，以该顶点为弧头的弧数目。
出度OD(v)：有向图中，以该顶点为弧尾的弧数目

仅1个顶点的入度为0,其余顶点的入度均为1时为树形

子图 对于图G=(V,E)和G’=(V’,E’)，如果V’属于V，E’属于E，且E’关联的顶点都在V’中，则称G’是G的子图。

生成子图 由图的全部顶点和部分边组成的子图称为原图的生成子图。

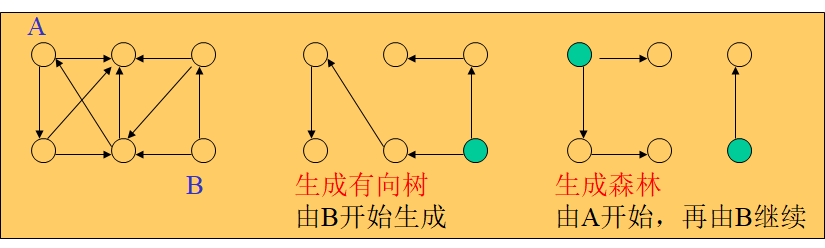
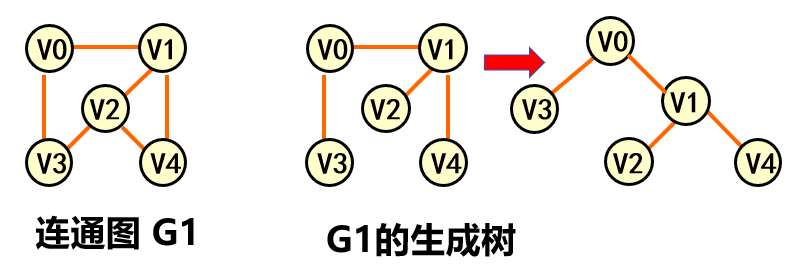
生成树 包含图中全部顶点的极小连通子图。

生成有向树 图中恰有一个顶点入度为0，其余顶点入度均为1。

生成森林 有向图中，包含所有顶点的若干棵有向树构成的子图。

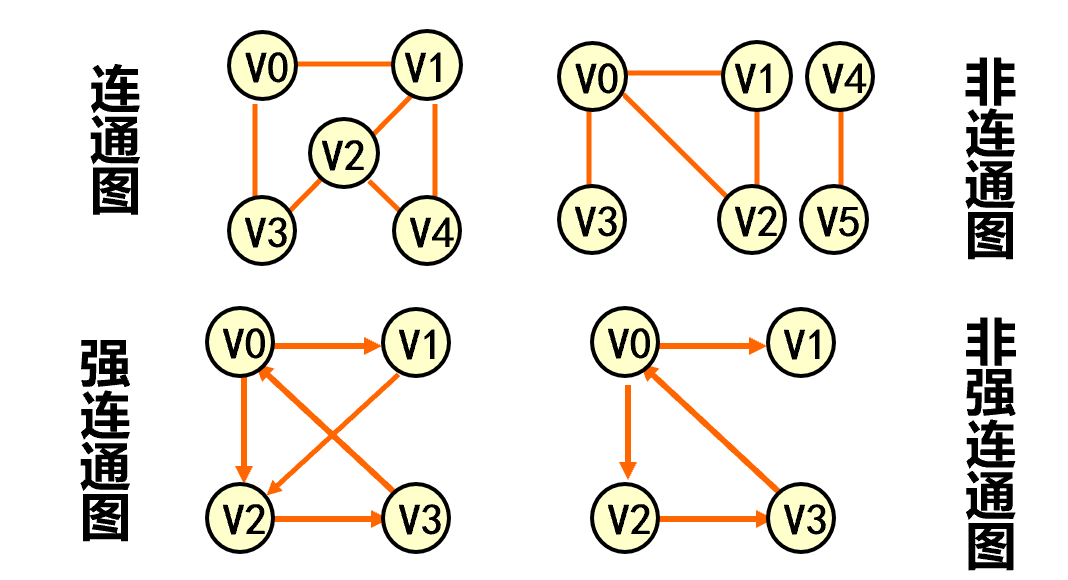
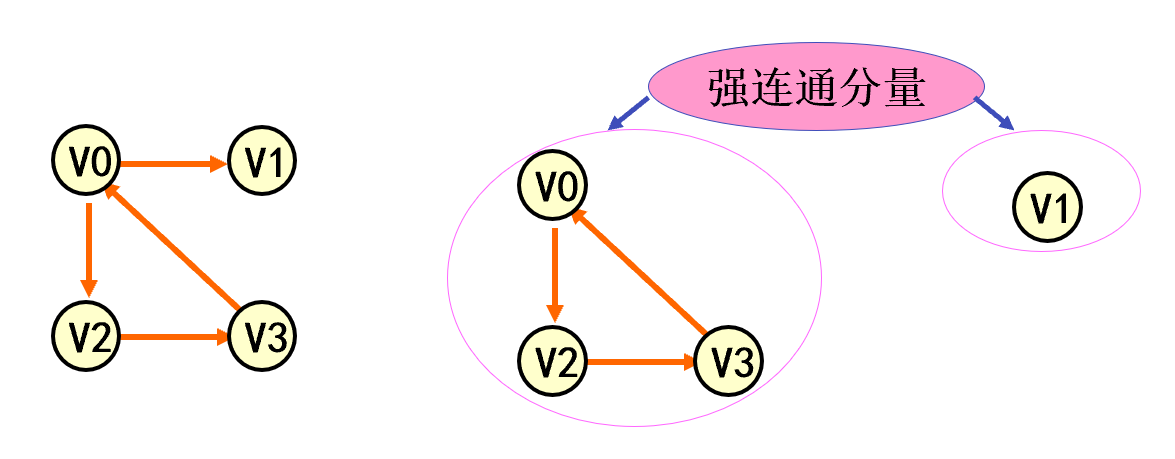
连通图（强连通图）

在无向图G=( V, {E} )中，若对任何两个顶点 v、u 都存在从v 到 u 的路径，则称G是连通图。

在有向图G=( V, {E} )中，若对任何两个顶点 v、u 都存在从v 到 u 的路径，则称G是连通图强连通图。

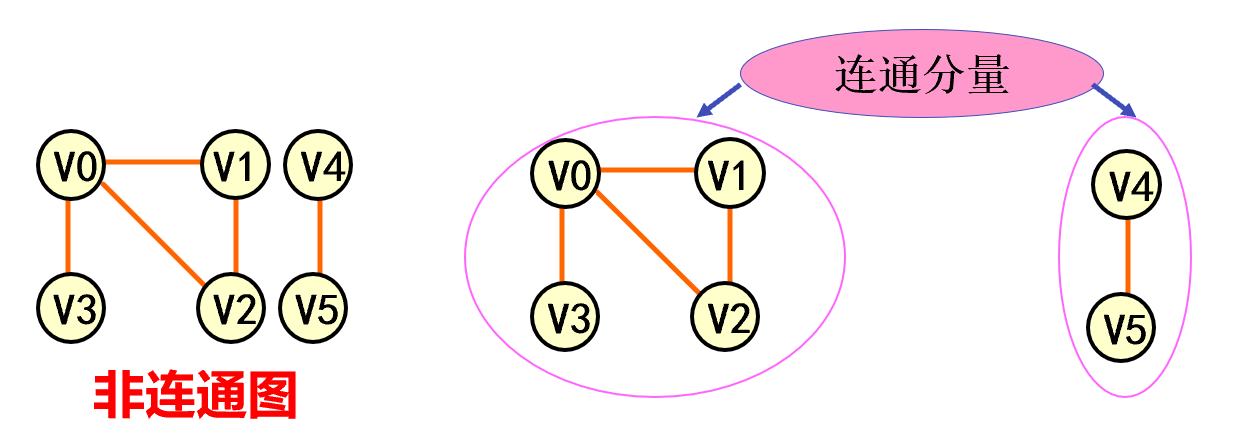
连通分量

无向图G 的极大连通子图称为G的连通分量。

极大连通子图意思是：该子图是 G 连通子图，将G 的任何不在该子图中的顶点加入，子图不再连通。

强连通分量

有向图G 的极大强连通子图称为G的强连通分量。极大强连通子图意思是：该子图是G的强连通子图，将G的任何不在该子图中的顶点加入，子图不再是强连通的。

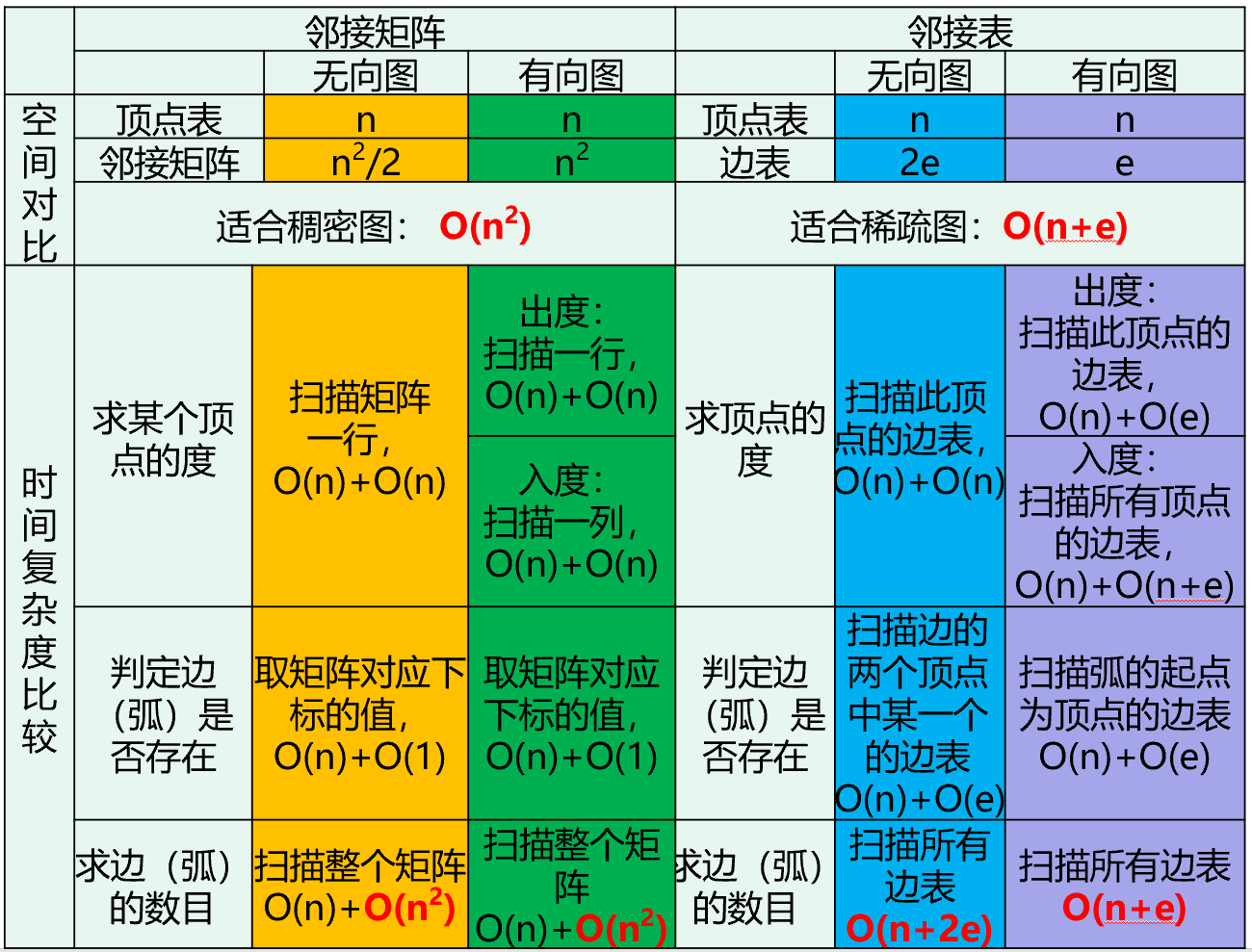
存储结构

顺序存储结构（数组表示法（邻接矩阵））

1. 建立一个顶点表（记录各个顶点信息）和一个邻接矩阵（表示各个顶点之间关系）。
2. 设图 A = (V, E) 有 n个顶点，则图的邻接矩阵是一个二维数组 A.Edge[n][n]，定义为：
   

邻接矩阵

无权图用1表示有边，0表示无边；网（有权图）用边权表示有边，∞表示无边

#define INFINITY         INT_MAX    // 最大值
#define MAX_VERTEX_NUM   20         // 最大顶点个数
typedef enum{DG, DN, UDG, UDN} GraphKind;   
        //有向图、有向网、无向图、无向网，四种图类型
typedef int VertexType;  //顶点携带信息的类型，假设为整数
typedef struct  ArcCell  {
    VRType      adj;  // 顶点关系类型，对无权图用0或1在矩阵中   
   //的行号和列号对应的顶点是否相邻。对带权图，则为边或弧的权值。
    InfoType  * info; // 该弧的相关信息指针
}ArcCell, AdjMatrix[MAX_VERTEX_NUM ][MAX_VERTEX_NUM ];
typedef struct   {
    VertexType  vexs[MAX_VERTEX_NUM];  // 顶点向量
    AdjMatrix   arcs;                  // 邻接矩阵
    int    vexnum, arcnum;          // 图的当前顶点数和弧数
    GraphKind   kind;               // 图的种类标志
}MGraph;

总结

优点：容易实现图的操作，如：求某顶点的度、判断顶点之间是否有边、找顶点的邻接点等等。

缺点：n个顶点需要n*n个单元存储边;空间效率为O(n^2)。

对稀疏图而言尤其浪费空间。

链式存储结构（多重链表）

邻接表、邻接多重表、十字链表

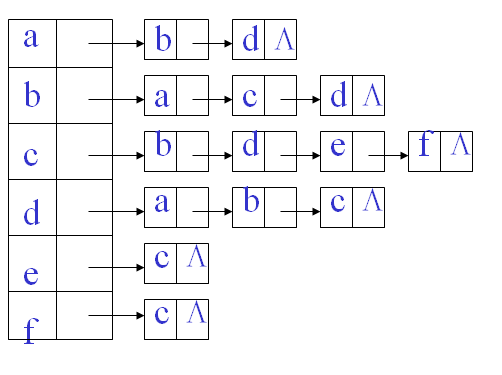
邻接表

图的一种顺序存储与链式存储结合的存储方法。

空间效率为：O(n+2e)

邻接表的逻辑概念：将顶点V的邻接点放入一个线性表(采用链式实现)存储

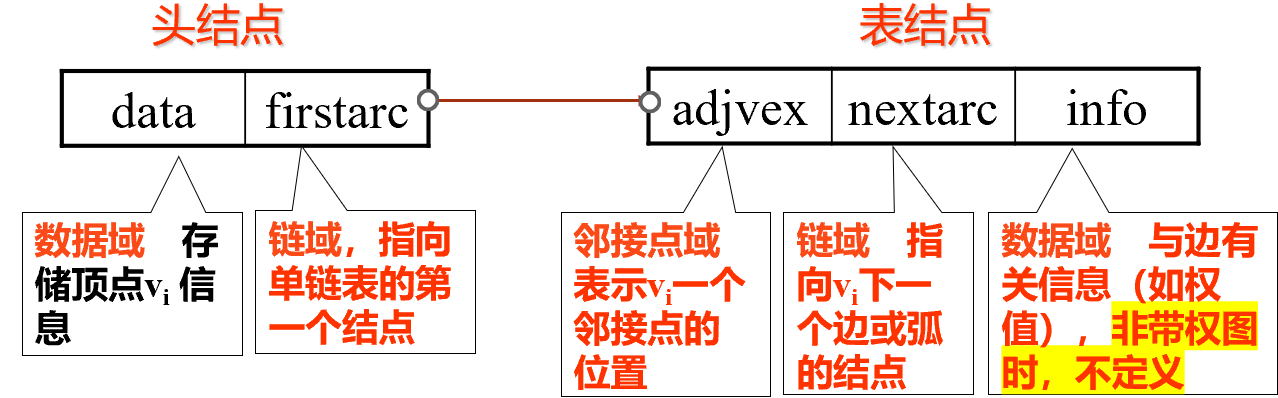
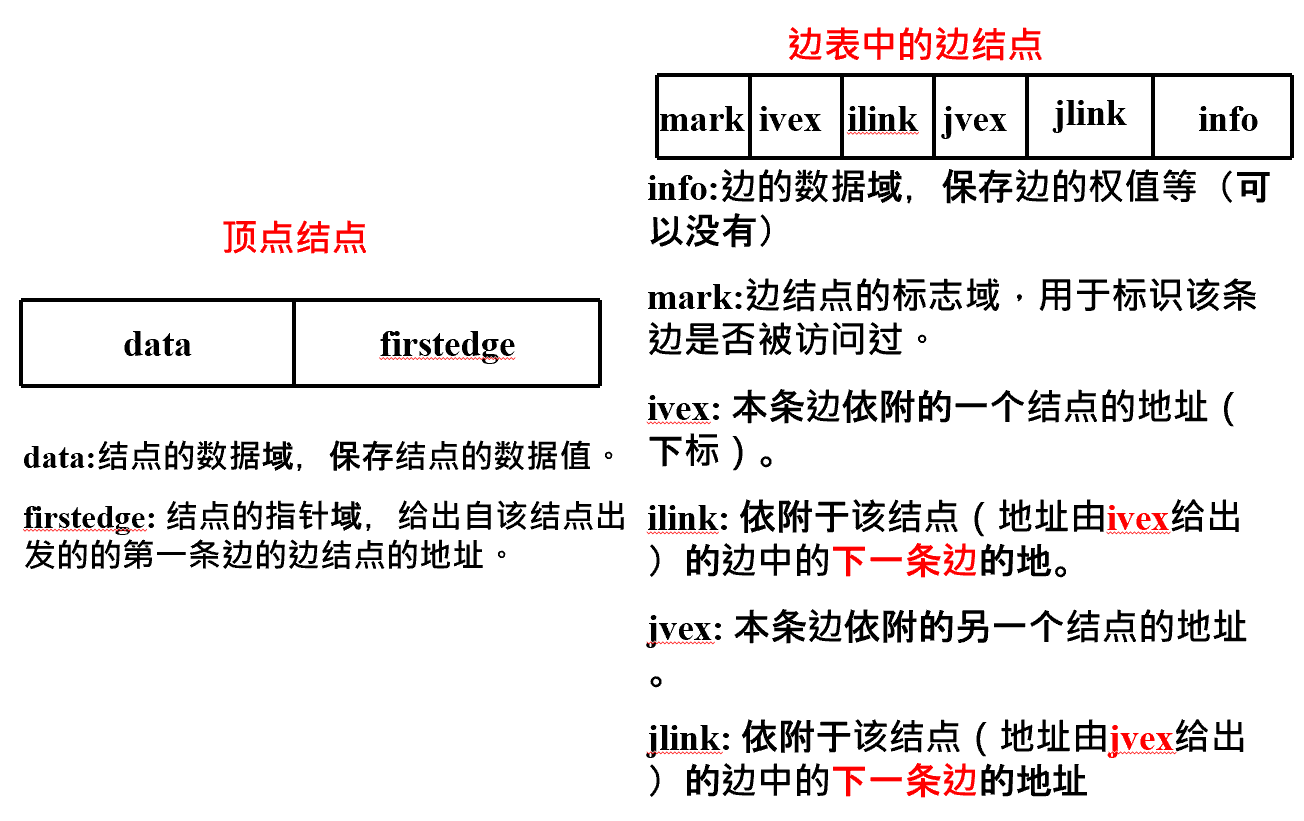
邻接表（链式）表示法

v对每个顶点vi 建立一个单链表，把与vi有关联的边的信息链接起来，每个结点设为3个域；边表。

每个单链表有一个头结点（设为2个域），存vi信息

用来记录顶点信息的头结点，用顺序存储结构保存为一个数组，顶点顺序表（顶点表）。

#define MAX_VERTEX_NUM   20                // 最大顶点个数
typedef enum{DG, DN, UDG, UDN} GraphKind;  // 四种图类型
typedef int VertexType;   //顶点携带信息的类型，假设为整数typedef struct  ArcNode  {
    int              adjvex;   //该边的另外一个顶点
                               //或弧所指向的顶点的位置
    struct ArcNode * nextarc ; //指向下一条边或弧的指针
    int              weight；  //边或弧的权重，网类型时使用
    InfoType       * info;     //该弧的其它相关信息的指针
}ArcNode；
typedef struct  VNode  {
    VertexType    data;     // 顶点信息
    ArcNode     * firstarc ;//指向第一条依附该顶点的弧
                            //或该顶点的第一条边的指针
                            /即头结点的指针域
}VNode, AdjList[MAX_VERTEX_NUM ];
typedef struct   {
    AdjList     vertices;        // 顶点向量
    int    vexnum, arcnum;       // 图的当前顶点数和弧数
    GraphKind   kind;            // 图的种类标志
}ALGraph;

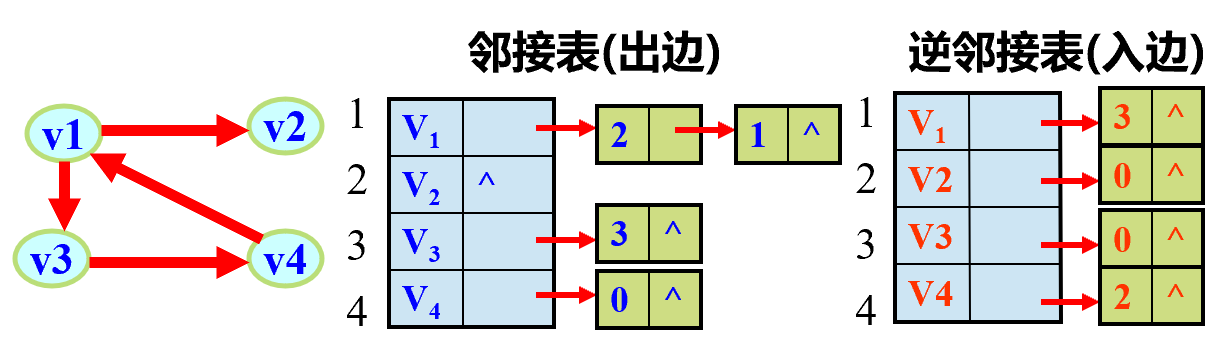
有向图的邻接表和逆邻接表

空间效率为O(n+e)

出度：OD(Vi)＝单链出边表中链接的结点数

入度：ID(Vi)＝邻接点域为Vi的弧个数

度：TD(Vi) = OD( Vi ) + I D( Vi )

十字链表

适用对象为有向图，顺序存储+链式存储

对矩阵中每个非零元素存储为一个结点，结点由5个域组成，其中：row域存储非零元素的行号，col域存储非零元素的列号，v域存储本元素的值，right，down是两个指针域，从行方向、列方向链接起来。

核心思路：一条链表记录结点指向了谁，另一条链表记录谁指向了当前结点。

邻接多重表

适用对象为无向图，顺序存储+链式存储

核心思路：每条边对应一个结点，方便无向图中对边的操作。

图的遍历

(dfs)深度优先遍历 (树的先根遍历的推广)

(bfs)广度优先遍历 (树的按层次遍历的推广)

遍历定义：从已给的连通图中某一顶点出发，沿着一些边访遍图中所有的顶点，且使每个顶点仅被访问一次

深度优先搜索DFS

递归的算法思想

1. 访问顶点v，并记录v已被访问
2. 依次从v的未访问的邻接点出发，递归进行深度优先搜索图G
   2.1 先找到v的第一个邻接点w
   2.2 如果w存在并且w未访问过，对w进行递归的DFS，如果w不存在，递归函数返回。
   2.3 再从v的邻接点w出发，找下一个邻接点赋值到w
   2.4 回到2.2
3. 在顶点表中是否还有未访问的顶点，有则将未访问结点赋值到v，回到1；没有则算法结束。

只要将v的邻接点都递归访问完，那么v所在的连通分量中的顶点就都会被访问到。对非连通图，依次对每个连通分量进行就可以完成图的DFS

非递归的算法思想

1. 访问一个顶点，并记录它已被访问；将它的所有未访问的邻接顶点入栈
2. 如果栈空，则退出；否则，栈中一顶点出栈；
3. 如果该顶点已被访问过，则转2 否则，转1

广度(宽度)优先遍历BFS

算法思想：

1. 访问顶点v，并记录它已被访问；顶点v入队列；
2. 如果队列空，则退出；否则，从队中取出一顶点
3. 求该顶点的一个邻接点；如果此邻接点未被访问，则访问它，并记录它已被访问，将其入队列；
4. 如果该顶点还有下一个邻接点，则转(3)；否则，转(2)

连通性问题

子图相关术语

生成子图 由图的全部顶点和部分边组成的子图称为原图的生成子图。

极小连通子图 该子图是G 的连通子图，在该子图中删除任何一条边，子图不再连通。
与上文种极大连通子图对应，一个是加入不连通，一个是减少不连通

生成树 包含无向图G 所有顶点的极小连通子图。

生成森林 对非连通图，由各个连通分量的生成树的集合。

生成树的概念（从遍历的角度看）

设G=(Vn,En)，则从图中任一顶点进行遍历图时，必定将En分成两个集合T(G)和B(G)，其中T(G)是遍历时经过的边的集合，B(G)是剩余边的集合。T(G) 是的G的一棵生成树。因此只有n-1条边

因此，一个图的生成树是不唯一的

• 因为可能从不同的顶点出发
• 采用不同的存储结构何存储顺序

对于非连通图，通过这样的遍历，将得到的是生成森林

最小生成树

在网的多个生成树中，寻找一个各边权值之和最小的生成树，记为MST(Minimum Cost Spanning Tree)。

基本准则：

• 必须只使用该网中的边来构造最小生成树；
• 必须使用且仅使用n-1条边来联结网络中的n个顶点
• 不能使用产生回路的边

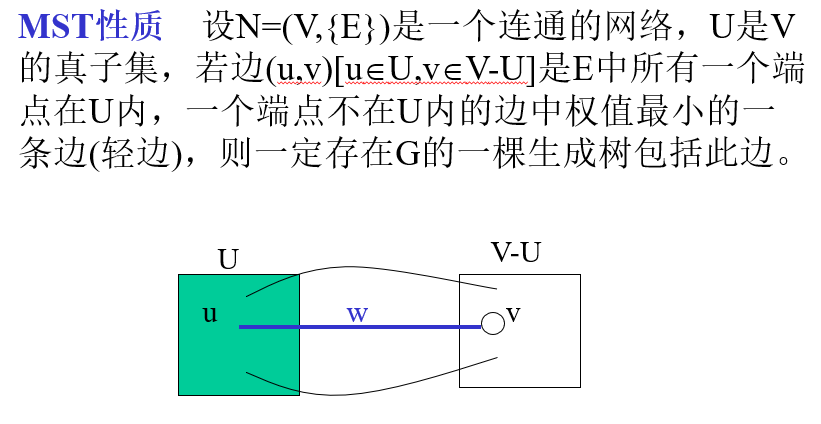
MST性质

生成树一定包含最短连通边？

Prim算法

归并顶点，与边数无关，适于稠密网

1. 将图中顶点分为两个集合，其中集合 X 包含图的一个顶点 v0，集合 Y 包含除 v0 外的其它所有顶点；（起始只有一个顶点）
2. 将跨接这两个集合的权值最小的边加入生成树中，并将其依附在集合 Y 中的顶点 v1 从 Y 中移入集合 X 中；**(找可以连接到目前生成树上的最短边及此边连入的顶点)**
3. 反复过程 2，直到集合 Y 为空，所得生成子图即为最小生成树。

存储结构

主空间：带权邻接矩阵G.arcs[n][n]的记录图

辅助空间（记录候选边）：数组closedge[i] (i=0…n-1)
- lowcost，当前vi的轻取边值
- adjvex，该边依附的U集合中的顶点下标（连接时确认边的两个顶点）

算法步骤

调整方法：U中新增顶点k带来的和j关联的边(k,j)权值小就替换已有候选边，因closedge[j]中记录了现在为止权值最小边，新增边与其比较选一个小的即可

以下是O(n^2)算法

void Prim(MGraph G, VertexType u ) 
{ 
  //用v和其他结点的边权值初始化辅助数组
  k=LocateVex(G,u);
  for(j=0; j<G.vexnum; ++j)  //即为v结点在邻接矩阵的k行数据
    closedge[j]={k, G.arcs[k][j].adj};
  //在剩余结点中循环,
  //依次找出最小生成树的边权值最小并且连接U和V-U的边和结点
  for (i=1; i<G.vexnum; ++i)  {   //进行G.vexnum-1次循环
    k=minium(closedge); //选择权值最小的边对应的V-U中的顶点
    printf(closedge[k].adjvex, k);
    closedge[k].lowcost=0;     //顶点k并入U集
    for (j=0; j<G.vexnum; ++j) //用k带来的边调整候选边
      if (G.arcs[k][j].adj<closedge[j].lowcost)
        closedge[j]={k, G.arcs[k][j].adj};
  }
}//Prim

Kruskal算法

归并边，适于稀疏网

1. 将图中所有边按权值从小到大排序；只使用所有的顶点形成图（n个顶点情况下，形成n个连通分量，即所有顶点互不连通）；
2. 取权值最小的边，加入图中，判断是否形成了回路，未形成回路则保留此边；否则去掉该边，重取权值较小的边；（方法：选两个顶点落在不同的连通分量上的最小权值的边）
3. 反复过程2，直到全部顶点均连通为止。

void MiniSpanTree_Kruskal(MGraph G) {
    int parent[MAXVEX];  // 用于判断边与边是否形成环路
    Edge edges[MAXVEX];  // 存储所有边
    int edgeCount = 0;

    // 初始化parent数组
    for (int i = 0; i < G.numVertexes; i++) {
        parent[i] = 0;
    }

    // 将图中的所有边存储到edges数组中
    for (int i = 0; i < G.numVertexes; i++) {
        for (int j = i + 1; j < G.numVertexes; j++) {
            if (G.arcs[i][j] != INFINITY) {
                edges[edgeCount].begin = i;
                edges[edgeCount].end = j;
                edges[edgeCount].weight = G.arcs[i][j];
                edgeCount++;
            }
        }
    }

    // 按权值对边进行排序
    for (int i = 0; i < edgeCount - 1; i++) {
        for (int j = i + 1; j < edgeCount; j++) {
            if (edges[i].weight > edges[j].weight) {
                Edge temp = edges[i];
                edges[i] = edges[j];
                edges[j] = temp;
            }
        }
    }

    printf("边 \t权重\n");

    // 选择边并构建最小生成树
    for (int i = 0; i < edgeCount; i++) {
        int n = Find(parent, edges[i].begin);
        int m = Find(parent, edges[i].end);

        if (n != m) {
            Union(parent, n, m);
            printf("(%c, %c) \t%d\n", G.vexs[edges[i].begin], G.vexs[edges[i].end], edges[i].weight);
        }
    }
}

在Kruskal算法中，判断图中是否产生回路的依据是使用并查集（Union-Find）数据结构。

int Find(int *parent, int f) {
    while (parent[f] > 0)
        f = parent[f];
    return f;
}
void Union(int *parent, int i, int j) {
    parent[i] = j;
}

破圈法

1. 在图中找到一个回路
2. 去掉该回路中权值最大的边
3. 反复此过程，直到图中不存在回路为止

去边法（感觉跟破圈没多大区别）

1. 将图中所有边按权值从大到小排序
2. 去掉权值最大的边，若图不再连通则保留此边，再选取下一权值较大的边去掉
3. 反复此过程，直到图中只剩下n-1条边

完整代码

#include <stdio.h>
#include <limits.h>

#define MAXVEX 100  // 最大顶点数
#define INFINITY INT_MAX  // 表示无穷大

typedef char VertexType;  // 顶点类型
typedef int EdgeType;     // 边上的权值类型

typedef struct {
    VertexType vexs[MAXVEX];  // 顶点表
    EdgeType arcs[MAXVEX][MAXVEX];  // 邻接矩阵
    int numVertexes, numEdges;  // 图中当前的顶点数和边数
} MGraph;

typedef struct {
    VertexType adjvex;  // 依附的U集合中的顶点
    EdgeType lowcost;   // 当前轻取边的权值
} Closedge[MAXVEX];

void Prim(MGraph G, VertexType u) {
    Closedge closedge;
    int k = 0;

    // 初始化closedge数组
    for (int j = 0; j < G.numVertexes; j++) {
        if (j != u) {
            closedge[j].adjvex = u;
            closedge[j].lowcost = G.arcs[u][j];
        }
    }
    closedge[u].lowcost = 0;  // 初始顶点u加入U集合

    // 选择n-1条边
    for (int i = 1; i < G.numVertexes; i++) {
        int min = INFINITY;
        for (int j = 0; j < G.numVertexes; j++) {
            if (closedge[j].lowcost != 0 && closedge[j].lowcost < min) {
                min = closedge[j].lowcost;
                k = j;
            }
        }

        // 输出当前选择的边
        printf("边 (%c, %c) 权值: %d\n", G.vexs[closedge[k].adjvex], G.vexs[k], closedge[k].lowcost);
        closedge[k].lowcost = 0;  // 将k加入U集合

        // 更新closedge数组
        for (int j = 0; j < G.numVertexes; j++) {
            if (G.arcs[k][j] < closedge[j].lowcost) {
                closedge[j].adjvex = k;
                closedge[j].lowcost = G.arcs[k][j];
            }
        }
    }
}

int main() {
    MGraph G;
    G.numVertexes = 5;
    G.numEdges = 7;

    // 初始化顶点
    G.vexs[0] = 'A';
    G.vexs[1] = 'B';
    G.vexs[2] = 'C';
    G.vexs[3] = 'D';
    G.vexs[4] = 'E';

    // 初始化邻接矩阵
    int arcs[MAXVEX][MAXVEX] = {
        {0, 2, INFINITY, 6, INFINITY},
        {2, 0, 3, 8, 5},
        {INFINITY, 3, 0, INFINITY, 7},
        {6, 8, INFINITY, 0, 9},
        {INFINITY, 5, 7, 9, 0}
    };

    for (int i = 0; i < G.numVertexes; i++) {
        for (int j = 0; j < G.numVertexes; j++) {
            G.arcs[i][j] = arcs[i][j];
        }
    }

    // 从顶点A开始计算最小生成树
    Prim(G, 0);

    return 0;
}

#include <stdio.h>
#include <stdlib.h>

#define MAXVEX 100  // 最大顶点数
#define INFINITY 9999  // 表示无穷大

typedef char VertexType;  // 顶点类型
typedef int EdgeType;     // 边上的权值类型

typedef struct {
    VertexType vexs[MAXVEX];  // 顶点表
    EdgeType arcs[MAXVEX][MAXVEX];  // 邻接矩阵
    int numVertexes, numEdges;  // 图中当前的顶点数和边数
} MGraph;

typedef struct {
    int begin, end;  // 边的两个顶点
    EdgeType weight; // 边的权值
} Edge;

int Find(int *parent, int f) {
    while (parent[f] > 0)
        f = parent[f];
    return f;
}

void Union(int *parent, int i, int j) {
    parent[i] = j;
}

void MiniSpanTree_Kruskal(MGraph G) {
    int parent[MAXVEX];  // 用于判断边与边是否形成环路
    Edge edges[MAXVEX];  // 存储所有边
    int edgeCount = 0;

    // 初始化parent数组
    for (int i = 0; i < G.numVertexes; i++) {
        parent[i] = 0;
    }

    // 将图中的所有边存储到edges数组中
    for (int i = 0; i < G.numVertexes; i++) {
        for (int j = i + 1; j < G.numVertexes; j++) {
            if (G.arcs[i][j] != INFINITY) {
                edges[edgeCount].begin = i;
                edges[edgeCount].end = j;
                edges[edgeCount].weight = G.arcs[i][j];
                edgeCount++;
            }
        }
    }

    // 按权值对边进行排序
    for (int i = 0; i < edgeCount - 1; i++) {
        for (int j = i + 1; j < edgeCount; j++) {
            if (edges[i].weight > edges[j].weight) {
                Edge temp = edges[i];
                edges[i] = edges[j];
                edges[j] = temp;
            }
        }
    }

    printf("边 \t权重\n");

    // 选择边并构建最小生成树
    for (int i = 0; i < edgeCount; i++) {
        int n = Find(parent, edges[i].begin);
        int m = Find(parent, edges[i].end);

        if (n != m) {
            Union(parent, n, m);
            printf("(%c, %c) \t%d\n", G.vexs[edges[i].begin], G.vexs[edges[i].end], edges[i].weight);
        }
    }
}

int main() {
    MGraph G;
    G.numVertexes = 5;
    G.numEdges = 7;

    // 初始化顶点
    G.vexs[0] = 'A';
    G.vexs[1] = 'B';
    G.vexs[2] = 'C';
    G.vexs[3] = 'D';
    G.vexs[4] = 'E';

    // 初始化邻接矩阵
    int arcs[MAXVEX][MAXVEX] = {
        {0, 2, INFINITY, 6, INFINITY},
        {2, 0, 3, 8, 5},
        {INFINITY, 3, 0, INFINITY, 7},
        {6, 8, INFINITY, 0, 9},
        {INFINITY, 5, 7, 9, 0}
    };

    for (int i = 0; i < G.numVertexes; i++) {
        for (int j = 0; j < G.numVertexes; j++) {
            G.arcs[i][j] = arcs[i][j];
        }
    }

    // 计算并打印最小生成树
    MiniSpanTree_Kruskal(G);

    return 0;
}

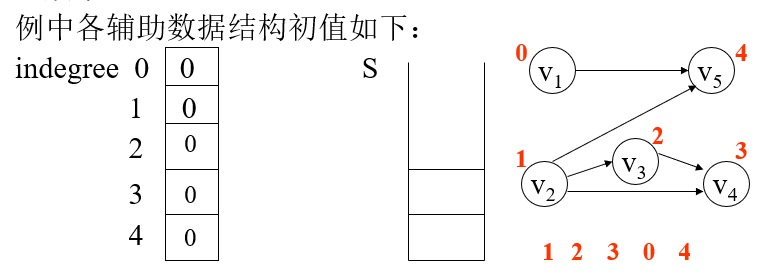
有向无环图及其应用（DAG,Directed Acyclic Graph ）

拓扑排序

照有向图给出的次序关系，将图中顶点排成一个线性序列。

检查有向图中是否存在回路的方法之一，是对有向图进行拓扑排序。如果不能进行拓扑排序，则证明该图中存在回路

无前趋的顶点优先算法

在一个拓扑序列中，每个顶点必定出现在它的所有前趋顶点之后。

1. 选择一个入度为0的顶点(无前趋的顶点)，输出它
2. 删去该顶点及其关联的所有出边

重复上述两步，直至图中不再有入度为0的顶点为止。
若所有顶点均被输出，则排序成功，否则图中存在有向环。

若该有向图不是无环图，则不存在拓扑排序。可以来判断一个有向图是否存在回路。

数据结构

• 一维数组indegree[0..n-1]：记录每个顶点的当前入度
• 栈S（或者队列Q）：暂存当前所有待输出的入度为0的顶点。作用是避免每次扫描indegree，提高算法效率。

算法步骤

1. 初始化辅助数据结构
   1. 扫描邻接表G的各出边表，在indegree中计数；O(n+e)
   2. 检查indegree数组，将入度为0的顶点入栈； O(n)
   3. 输出顶点计数器 count= 0； O(1)
2. 若栈不空，反复执行以下操作
   1. 栈顶元素i出栈； O(n)
   2. 输出顶点i，count加 1； O(n)
   3. 扫描顶点i的出边表： O(n+e)
      修改indegree，将出边表上顶点的入度减 1；
      若其入度为 0，则令其入栈
3. 若count<顶点数vexnum则出现回路排序失败

Status TopologicalSort(ALGraph G) 
{ FindInDegree(G,indegree);//求各顶点入度indegree[G.vexnum]
  InitStack(S);  // InitQueue(Q);
  for (i=0; i<G.vexnum; ++i)  
    if (!indegree[i]) push(S, i);  // EnQueue(Q,i)         
  count=0;
  while (! StackEmpty(S))   // (!QueueEmpty(Q))
  {
    pop(S, i); //DeQueue(Q, i);
    printf(i, G.vertices[i].data); ++count;
    for(p=G.vertices[i].firstarc;p;p=p->nextarc)  
    {  //修改入度
       k=p->adjvex;
       //入度为0则入栈(入队列)
       if(!(--indegree[k])) push(S,k); //EnQueue(Q,i) 
    }//for
  }//while
  if (count<G.vexnum) return ERROR;  
  else return OK;
}//TopologicalSort

无后继的顶点优先算法

按逆拓扑次序生成顶点序列

在一个拓扑序列中，每个顶点必定出现在它的所有后继顶点之前

1. 选择一个出度为0的顶点(无后继的顶点)，输出它
2. 删去该顶点及其关联的所有入边

重复上述两步，直至图中不再有出度为0的顶点为止

Status TopologicalSort(ALGraph G) 
{ 
  FindInDegree(G,outdegree);//求各顶点出度outdegree[G.vexnum]
  InitStack(S);
  for (i=0; i<G.vexnum; ++i)  
    if (! outdegree[i]) push(S, i);         
  count=0;
  while (! StackEmpty(S)) 
  {
    pop(S, i); printf(i, G.vertices[i].data); ++count;

    //对 G.vertices[i] 顶点，找其“弧尾/初始点”k
    //修改k的出度
    //若k的出度为0，k入栈

  }//while
  if (count<G.vexnum) return ERROR;  
  else return OK;
}//TopologicalSort

利用深度优先遍历（从入度为0的顶点出发）

1. 访问顶点v，并记录v已被访问
2. 依次从v的未访问的邻接点出发，深度优先拓扑排序图G。
3. 输出顶点v（此时v相当于无后继的顶点）

此方法仅适用于有向无环图（此算法不能检测出有向环，得到虚假拓扑序列）

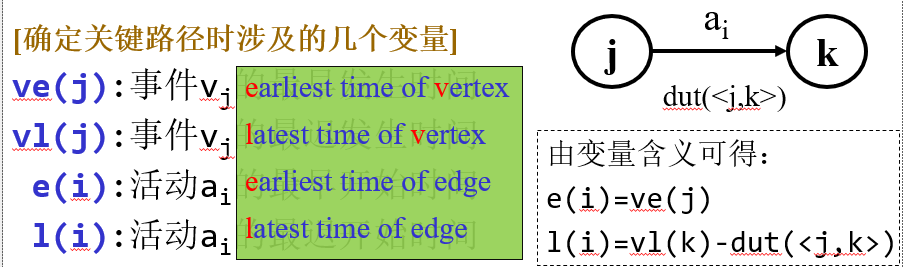
关键路径

顶点(vertex)用来表示事件(event)，弧(edge)用来表示活动(activity)，权值表示活动所需时间(dut)，称为边活动图(activityon edge network)，简称AOE网(AOE图)。

[AOE网的性质]

• 进入Vi的活动都结束，Vi所代表的事件才能发生
• 顶点Vi所代表的事件发生，从Vi出发的活动才能开始

相关概念和术语

源点 入度为0的顶点，即工程的开始点

汇点 出度为0的顶点，即工程的完成点

活动持续时间 活动ai由弧<j,k>表示，用dut(<j,k>)表示持续时间

关键路径 从源点到汇点的最长路径，关键路径长度=最短工期

关键活动 关键路径上的活动，关键活动的加快可以缩短工期

对于每个活动，如果它的最早发生时间等于最迟发生时间，那么这个活动就是关键活动。连接所有关键活动，就形成了关键路径。

关键活动的判断方法：e(i)=l(i)

算法步骤

辅助数组：ve(0..n-1), vl(0..n-1)，e(0..m-1), l(0..m-1)
{n为图的顶点数目；m为图的弧数目}

T表示栈，存储拓扑排序的顶点序列

1. 输入所有弧的信息，建立AOE网的存储结构
2. 计算ve[]数组值，事件的最早开始时间：
   1. 先进行拓扑排序，得到一个顶点的线性序列，满足：如果存在一条从顶点u到顶点v的有向边，那么在序列中u一定排在v的前面。
   2. 每求得一个顶点j，则使j入栈T，并调整j的所有后继的ve值
3. 计算vl[]数组值，事件的最迟开始时间：
   从终止顶点开始，逆着拓扑排序的顺序，即利用栈T
   按栈T的从栈顶到栈底的顺序求顶点的vl值
4. 计算e[] 和l[]数组值，活动的最早开始时间和最迟开始时间
   求每个活动i的e(i)和l(i)值；

依据e(i)=l(i) 确定关键事件，再确定关键路径

最早发生时间ve(j)

ve(0)=0
ve(j)=max{ve(i)+dut(<i,j>)}(i属于j的前驱)

1. 初值ve[j]=0 0<=j<=n-1
2. 每输出一个无前驱的顶点j后，修正j的所有后继结点k的

最迟发生时间vl(j)

vl(n-1)=ve(n-1){保证ve(n-1)的前提下}
vl(j)=min{vl(k)- dut(<j,k>)} (k属于j的后继)

此时按逆拓扑序列逐一计算

1. 初值vl[j]=ve[j] 0<=j<=n-1
2. 按拓扑排序结果，逆序计算 min{vl(k)- dut(<j,k>)}

求活动ai的最早开始时间e(i)和最迟开始时间l(i)

确定关键活动e(i)=l(i)

e(i)=ve(j)
l(i)=vl(k)-dut(<j,k>)

算法描述

Status TopologicalOrder(ALGraph G, Stack &T, int * ve) 
//计算各顶点的最早发生时间保存在ve中，并用栈T返回G的一个拓扑序列
{  
  FindInDegree(G, indegree);//求各顶点入度indegree[G.vexnum]
  InitStack(S); count=0; ve[0..G.vexnum-1]=0; 
  for (i=0; i<G.vexnum; ++i)  if (! indegree[i]) push(S, i); 
  InitStack(T);
  while (! StackEmpty(S)) {
    pop(S, j); push(T, j); ++count;
    for (p=G.vertices[j].firstarc; p; p=p->nextarc){
      k=p->adjvex;
      if (! (--indegree[k])) push(S,k);  //若入度为0则入栈
      if (ve[j]+(p->weight) > ve[k]) ve[k]= ve[j]+(p->weight);
    }//for
  }//while
  if (count<G.vexnum) return ERROR;  else return OK;
}//TopologicalOrder

Status CriticalPath(ALGraph G) 
//G为有向网，输出G的各项关键活动
{ if (! TopologicalOrder(G,T,ve) ) return ERROR;
  vl[0.. G.vexnum-1] = ve[G.vexnum-1] ;
  while (! StackEmpty(T)){   //按拓扑逆序求各顶点的vl值
    for ( pop(T, j), p=G.vertices[j].firstarc; p; p=p->nextarc) { 
      k=p->adjvex;
      if (vl[k]-(p->weight) < vl[j]) vl[j]= vl[k]-(p->weight);
    }//for
    for (j=0; j<G.vexnum; ++j){  //求各活动的ee、el和确定关键活动
      for (p=G.vertices[j].firstarc; p; p=p->nextarc) {
        k=p->adjvex;  dut=p->weight;
        ee=ve[j]; el=vl[k]-dut;
        tag=(ee==el) ? ’*’ :’ ’;
        printf(j, k, dut, ee, el, tag);
      } //for
    } //for
  } //while
}//CriticalPath

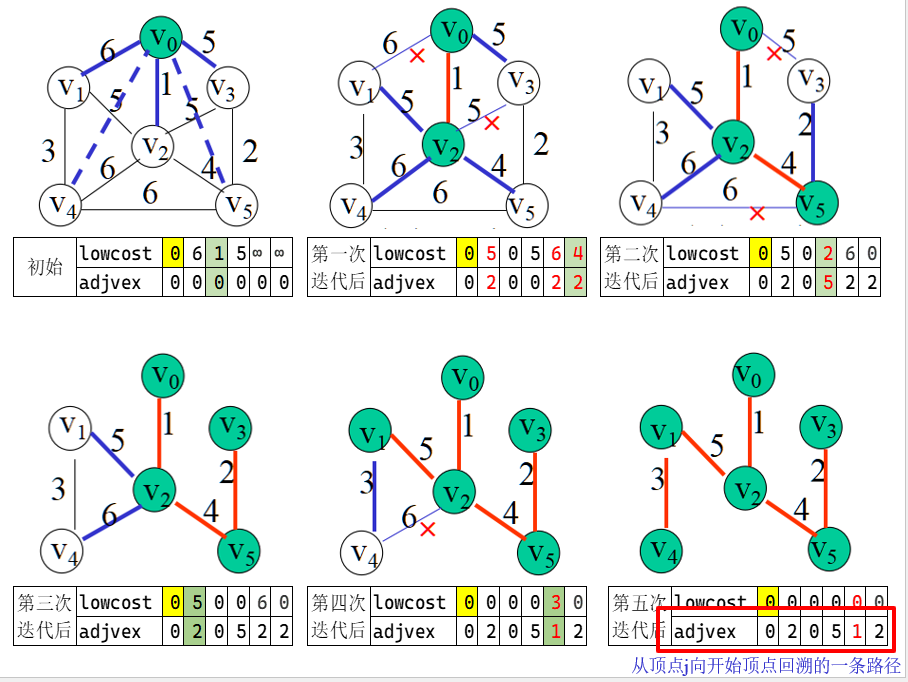
7.6 最短路径

Dijkstra

局限性：

• 不能处理负权边： Dijkstra算法的核心思想是贪心算法，它假设每次选取距离源点最近的未访问节点进行扩展。但在存在负权边的情况下，这种贪心策略可能导致错误的结果。
• 适用于稀疏图： 对于稠密图，Dijkstra算法的时间复杂度可能会较高。

void ShortestPath_DIJ( Mgraph G,int v0, 
                       PathMatrix &P, ShortPathTable &D)
{   for (v = 0; v < vexnum; v++) {
        final[v] = FALSE; D[v] = G.arcs[v0][v];
        for (w = 0; w < vexnum; w++) P[v][w] = FALSE;
        if (D[v] < INFINITY)  P[v][v0] = p[v][v] = TRUE;
    }
    D[v0] = 0;   final[v0] = TRUE;
    for (i = 1; i < vexnum; i++) {
        min = INFINITY;
        for (w = 0; w < vexnum; w++)
            if (!final[w] && D[w] < min) { k = w; min = D[w]; }
        final[k] = TRUE;
        /*考虑新加入的节点k */
        for (w = 0; w < vexnum; w++)
            if (!final[w] && (min + G.arcs[k][w] < D[w])) {
                D[w] = min + G.arcs[k][w];
                P[w] = P[k]; P[w][w] = TRUE;
            }
    }
}            

Floyd

设每个顶点都可以是中间顶点，通过该顶点都有可能使其它顶点间的距离缩短。因此，将所有顶点都作为中间顶点操作过一遍后，所得到的各顶点对间的距离即是最短距离，所得路径自然也就是最短路径了。该算法是求顶点间最短路径。

优点：

• 通用性强： Floyd算法可以处理任意图，包括带负权边的图，甚至可以检测到图中是否存在负权环。
• 求解所有顶点对之间的最短路径： Floyd算法可以一次性求解图中任意两个顶点之间的最短路径。

局限性：

• 时间复杂度高： Floyd算法的时间复杂度为O(V^3)，其中V是顶点的个数。对于大规模图，计算时间较长。
• 空间复杂度高： Floyd算法需要一个二维数组来存储所有顶点对之间的最短路径，空间消耗较大。

void ShortestPath_FLOYD2(Mgraph G, PathMatrix &P,
                              DistanceMatrix &D)
// P[v][w][k]为TRUE，则从v到w的最短路径中含有k节点
// D[v][w]从v到w的最短路径的长度
{  
  for (v = 0; v < n; v++)
    for (w = 0; w < n; w++) {
      D[v][w] = G.arcs[v][w];
      for (k = 0; k < n; k++) p[v][w][k] = FALSE;
      if (D[v][w] < INFINITY) 
        P[v][w][v] = P[v][w][w] = TRUE;
    }//for
  for (k = 0; k < n; k++) 
    for (v = 0; v < n; v++)
      for (w = 0; w < n; w++) 
        if (D[v][k] + D[k][w] < D[v][w]) {
          D[v][w] = D[v][k] + D[k][w];
            for (i = 0; i < n; i++)
              P[v][w][i] = P[v][k][i] || P[k][w][i];
        }//if
} // ShortestPath_FLOYD2        P191-算法7.16