静态查找表

查找表

同一类型的**记录(数据元素)**的集合

数据元素之间存在着松散的关系。为了提高查找的效率，可在元素之间人为地附加某种确定的关系。

• 静态查找表 对查找表的查找仅是以查询为目的，不改动查找表中的数据。
• 动态查找表 在查找的过程中同时插入不存在的记录，或删除某个已存在的记录。

关键字 记录(数据元素)中的某个数据项的值。

• 主关键字 该关键字可以唯一地标识一个记录。
• 次关键字 该关键字不能唯一标识一个记录。

查找

指定某个值，在查找表中确定是否存在一个记录，该记录的关键字等于给定值。

• 内查找 整个查找过程都在内存中进行，即全部数据元素均在内存。
• 外查找 在查找过程中需要访问外存，即数据元素需要分段读入内存查找。

平均查找长度ASL（ AverageSearch Length ）

静态查找表

静态查找表以顺序表表示

基础遍历

int Seq_Search_1 (datatype data[ ], keytype kx, int n)
{ /*查找表数据存放在data[1]至data[n]中，n是当前表中数据元素个数*/
  /*在表data中查找关键码为kx的数据元素，若找到返回该元素在数组中的下标，否则返回0*/

    int i=1;
    while(i<=n && data[i].key!= kx ) 
       i++;   /* 从表头端向后查找 */

    if (i>n) 
          return 0;
    else  
          return  i; 
 }

遍历（扫描）到线性表的一个数据元素时，要进行两次比较操作

但是如果将给定值放在第0个记录处，让遍历从高到低，从后往前查找，就不需要越界检查了（因此少了一半比较操作）

或者放在最高处n，从0遍历到n也一样

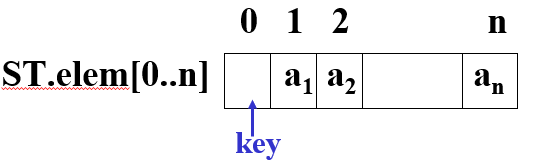
Int Seq_Search_2(datatype data[ ], keytype kx, int n)
{/*查找表数据存放在data[0]至data[n-1]中，n是当前表中数据元素个数*/
 /*在表data中查找关键码为kx的数据元素，若找到返回该元素在数组中的下标，否则返回-1*/
  
    //假设 n 小于等于 data数组长度 减一；在表尾设置哨兵
    data[n].key=kx;  
    i=0;                       //从0向后查找
    while(data[i].key!= kx )  i++;  /* 从表头向尾端查找 */
    if( i==n) return -1;
    else return i;
}   
    data[n]分量起到了监视哨的作用。
    这样一个小小的设计技巧，会大大提高查找效率。

有序表查找

而满足 r[i].key >=/<= r[i+1].key的有序表也同样可以设置哨兵值来协助查找

就 r[i].key <= r[i+1].key为例

1. 从前向后查找，哨兵设在尾部，当r[i]>=key时结束；
2. 从后向前查找，哨兵设在头部，当r[i]<=key时结束；

斐波那契查找

设查找表记录数为某个费波拉契数减一，即 n=Fu-1，则可将给定值与第Fu -1个记录比较，若比其小，则在1–Fu -1-1记录间查找，否则在Fu -1+1–Fu-1记录间查找 。如下图所示：

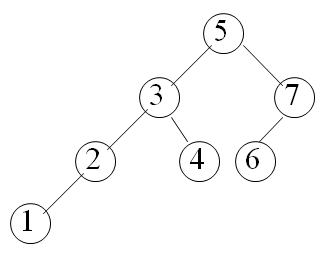
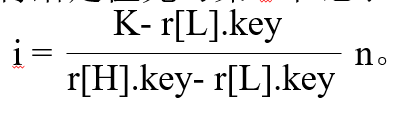
静态树的查找

两个原则

1. 最先访问的结点应是访问概率最大的结点；
2. 每次访问应使结点两边尚未访问的结点的被访概率之和尽可能相等。

静态最优查找树

定义：查找性能最佳的判定树

性质：带权内路径长度之和PH为最小值

其中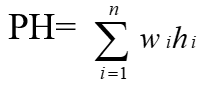与ASL成正比

n：二叉树上结点的个数(有序表长度)

hi：第i个结点在二叉树上的层次数

wi=c*pi：c为某个常量；

pi：第i个结点的查找概率

构造

由于构造最优查找树代价太大，转而构造次优查找树，两者性能相差不大

次优查找树的构造方法

首先我们有

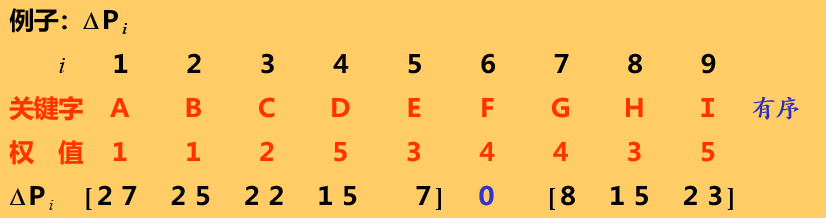
已知一个序列：(rl,rl+1,……，rh），递增有序。它对应的权值为：(wl,wl+1,……，wh)。

因此定义：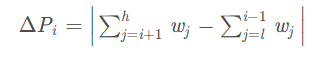

取 △Pi 最小的那个元素 i 作为根 ，然后分别对子序列（rl,rl+1,……，ri-1）和（ri+1,ri+2,……，rh）同样构造次优查找树，并将其分为左子树和右子树

在计算 △Pi 时，实际上就是计算元素 i 前面的元素的权值之和与元素i后面的元素的权值之和的差值

由于每次都需要重新计算一下前面的权值和后面权值之差，为提高效率，引入累计权值和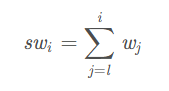

设 w(l-1) = 0 和 sw(l-1) = 0

则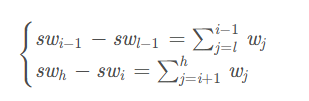

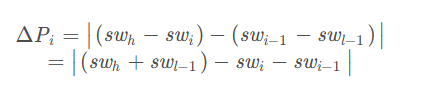
这样就把到第i个位置的累计权值和装入数组了，计算一次用多次。

次优查找树上的查找步骤

设给定的查找值为K

将根结点作为当前考察的结点

1）若当前结点指针为NULL，则返回空指针

2）将当前结点的关键字key与K比较，

• 若K=key，则返回当前结点的指针；
• 若K>key，将其右孩子作为当前结点，转1）；
• 若K<key，将其左孩子作为当前结点，转1）；

索引顺序表

分块查找（块间有序，块内无序）

分块有序：即分成若干子表，要求每个子表中的数值都比后一块中数值小（但子表内部未必有序）

各子表中的最大关键字构成索引表，表中还需要包含对应子表的起始地址

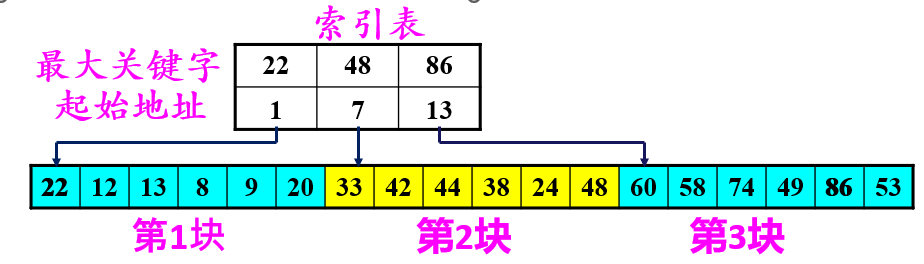
查找方法

1. 对索引表使用折半查找法（因为索引表是有序表）；
2. 确定了待查关键字所在的子表后，在子表内采用顺序查找法（因为各子表内部是无序表）；

索引顺序查找的平均查找长度 = 查找“索引”的平均查找长度 + 查找“块”的平均查找长度

• 顺序查找索引表+顺序查找被确定的块
  

  

• 折半查找索引表+顺序查找被确定的块