动态查找表

time will tell Lv4
  2024-11-28 09:11:59 2024-11-28 09:11:59 Created   2024-12-12 15:36:40 2024-12-12 15:36:40 Updated      

动态查找表

频繁进行插入、删除的查找表

二叉排序树BST

定义

安装左中右的顺序排序，左子树上所有结点的值均小于根结点的值，右子树上所有结点的值均大于根结点的值

中序遍历一棵二叉排序树，将得到一个以关键字递增排列的有序序列

操作

查找

查找就是从根节点开始，如果比根节点小就往左子树查找，反之往右子树查找，找到了或者结点为空时停止

非递归形式

1
2
3
4
5
6
7
8
9
10
11
12
Bitree  SearchBST ( BiTree T,  KeyType key )
//在二叉排序树T中查找关键字值为 key 的结点，
//找到返回该结点的地址，否则返回空。
{  
  if( (!T) || EQ(key, T->data.key)) 
    return T;
  else if ( LT(key, T->data.key)) 
    return (SearchBST(T->lchild, key));
  else 
    return (SearchBST(T->rchild, key)); 
} //SearchBST  P228-9.5（a）

递归形式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
bool SearchBST(BiTree T, KeyType key, BiTree f, BiTree &p)
//f指向当前结点的双亲,初始调用值为NULL。
//查找成功，p指向该结点，并返回TRUE；
//查找失败，p指向查找路径上的最后一个结点，并返回FALSE
{  
  if(!T)
  {
    p=f;  
    return FALSE;
  }
  else if EQ(key, T->data.key)
  {  
    p=T; 
    return TRUE; 
  }
  else if  LT(key, T->data.key) 
    return SearchBST(T->lchild, key, T, p);
  else 
    return SearchBST(T->rchild, key, T, p);
}//SearchBST   P228-9.5(b)

链表形式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
bool SearchBST(BiTree T, KeyType key, BiTree &p)
//查找成功，p指向该结点，并返回TRUE；
//查找失败，p指向查找路径上的最后一个结点，并返回FALSE
{  
  BiTree p = T;  //p作为工作指针
  BiTree q = NULL;//q用于跟踪p的双亲，根的双亲为NULL
  while(p)
  {
    if(EQ(key, p->data.key))
      return TRUE;

    q = p;
    if(LT(key, p->data.key))
      p = p->lchild;
    else 
      p = p->rchild; 
  }
  //此时q是空指针p的双亲结点，当需要插入key时即插入在q的下面；
  
  p = q; //将p置为q的值，返回
  return FALSE;
}

插入

插入则是在查找到的那个位置进行判断，一般如果在树中没有该元素时，查找到一个空结点，那么就可以直接插入

实际代码操作有一些不同

非递归形式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
bool InsertBST (BiTree &T,ElemType e) 
{ 
  if(!SearchBST(T, e.key, NULL, P)) 
  {
    s=(BiTree)malloc(sizeof(BiTNode));
    s->data=e;
    s->lchild=s->rchild=NULL;

    if(!T)  
      T=s;   //空二叉排序树
    else  if LT(e.key, p->data.key)
      p->lchild = s; //小则插到p的左孩子
    else 
      p->rchild = s; //大则插到p的右孩子
    return TRUE;
  }
  else 
    return FALSE
} //InsertBST   P228-9.6

这里用到了查找的递归形式，函数会在查找函数中没有找到该元素时先修改p结点为需要插入的上一个结点，然后再将p结点与需要插入的值进行判断，将其插入到左结点还是右结点

一步到位的形式为

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Status SearchBST(BiTree &T, KeyType key, BiTree &p)
{
  p = T;  //p用于返回key所在结点
  Bitree q=NULL; // q用于跟踪p的双亲，根的双亲为NULL
  while(p)
  {
    if(EQ(key, p->data.key))  { return OK; }
    q=p;
    if(LT(key, p->data.key)) { p = p->lchild;}
    else {p = p->rchild; }
  }
  //此时q是空指针p的双亲结点，当需要插入key时即在q的下面；
  if(!(p = (BiTree)malloc(sizeof(BiTNode))) return OVERSTACK;
  p->data=key; p->lchild=p->rchild=NULL;
  if(!T) //空树
    T = p; 
  else if(LT(key, q->data))
    q->lchild = p;
  else
    q->rchild = p;
  return OK;
}

同理，递归形式如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Status SearchInsertBST(BiTree T, BiTree f, KeyType key, BiTree &p)
//f指向当前结点的双亲,初始调用值为NULL。
//查找key成功，p指向该结点；查找key失败，插入keyy，p指向新结点，返回OK
{  
  if(!T) {
    if(!(p = (BiTree)malloc(sizeof(BiTNode)))) return OVERSTACK;
    p->data=key; p->lchild=s->rchild=NULL;
    if LT(key, f->data.key)    // 这里为什么不担心f为NULL？
      f->lchild = p; //小则成为f的左孩子
    else
      f->rchild = p; //大则成为f的右孩子
    return OK;
  }
  else if EQ(key, T->data.key){  
    p=T; return OK; 
  }
  else if LT(key, T->data.key) 
    return SearchInsertBST(T->lchild, T, key, p);
  else 
    return SearchInsertBST(T->rchild, T, key, p);
}

删除

删除结点被分为4种情况

  1. p是叶子结点：修改其双亲指针指向NULL即可
  2. p只有左孩子：用p的左子树代替以p为根的子树
  3. p只有右孩子：用p的右子树代替以p为根的子树
  4. p有两个孩子：找到p的中序后继(或前趋)结点q，q的数据复制给p
    此时需要递归处理q的删除问题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
Status DeleteBST(BiTree &T, KeyType key) {
    if (T == NULL) return ERROR; // 树为空，删除失败

    if (LT(key, T->data)) {//可用SearchBST代替
        return DeleteBST(T->lchild, key); // 在左子树中继续查找
    } else if (LT(T->data, key)) {
        return DeleteBST(T->rchild, key); // 在右子树中继续查找
    } 
    else { // 找到要删除的结点
        if (T->lchild != NULL && T->rchild != NULL) { // 结点有两个孩子
            BiTree temp = FindMin(T->rchild); // 找到右子树中的最小结点
            T->data = temp->data; // 用右子树中最小结点的值替换当前结点的值
            return DeleteBST(T->rchild, temp->data); // 删除右子树中的最小结点
            // 也可以用左子树中的最大结点替换当前结点，然后删除左子树中的最大结点
        } else { // 结点有一个或零个孩子
            BiTree temp = T;
            if (T->lchild == NULL) {
                T = T->rchild; // 用右孩子替换当前结点
            } else if (T->rchild == NULL) {
                T = T->lchild; // 用左孩子替换当前结点
            }
            free(temp); // 释放当前结点
            return OK;
        }
    }
}
BiTree FindMin(BiTree T) {
    if (T == NULL) return NULL; // 如果树为空，返回 NULL
    while (T->lchild != NULL) {
        T = T->lchild; // 一直向左子树遍历，直到找到最左边的结点
    }
    return T; // 返回最左边的结点，即最小值结点
}

平衡二叉树（AVL树）

关键字有序出现时，将构造出“退化”的二叉排序树，这使得查找的效率降低，为避免这种情况发生，需要采用平衡二叉树

定义

空树，或者是满足如下性质的二叉排序树：

  1. 左、右子树的高度之差的绝对值不超过1
    $|ℎ_𝐿−ℎ_𝑅 |≤1$
  2. 左右子树本身又各是一棵平衡二叉树

引入一个平衡因子的概念

二叉树上结点的平衡因子：该结点的左子树高度减去右子树的高度

但是不得不承认，平衡二叉树不一定是理想的最矮状态

查找的分析

一个具有n个结点的平衡二叉树的最大深度h为

$$
log_a(sqrt(5)*(n+1))-2
$$

其中a

$$
a=(1+sqrt(5))/2
$$

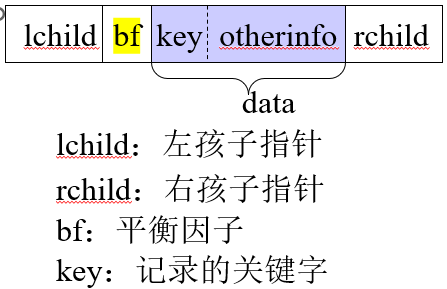
结点的存储结构

1732759763148

1
2
3
4
5
6
7
8
9
10
11
typedef  struct {
     KeyType key;
     ……
}ElemType
typedef struct BSTNode {
  ElemType  data;
  int  bf;
  struct BSTNode *lchild,
                 *rchild;
}BSTNode, * BSTree;

平衡二叉树上的操作

1、结点高度

结构中已经确认添加了结点高度height，对于每个结点都有如下定义

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/* AVL 树节点结构体 */
typedef struct TreeNode {
    int val;
    int height;
    struct TreeNode *left;
    struct TreeNode *right;
} TreeNode;

/* 构造函数 */
TreeNode *newTreeNode(int val) {
    TreeNode *node;

    node = (TreeNode *)malloc(sizeof(TreeNode));
    node->val = val;
    node->height = 0;
    node->left = NULL;
    node->right = NULL;
    return node;
}

“节点高度”是指从该节点到它的最远叶节点的距离，即所经过的“边”的数量。需要特别注意的是，叶节点的高度为 0 ，而空节点的高度为 −1 。我们将创建两个工具函数，分别用于获取和更新节点的高度：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/* 获取节点高度 */
int height(TreeNode *node) {
    // 空节点高度为 -1 ，叶节点高度为 0
    if (node != NULL) {
        return node->height;
    }
    return -1;
}

/* 更新节点高度 */
void updateHeight(TreeNode *node) {
    int lh = height(node->left);
    int rh = height(node->right);
    // 节点高度等于最高子树高度 + 1
    if (lh > rh) {
        node->height = lh + 1;
    } else {
        node->height = rh + 1;
    }
}

2、结点平衡因子

设平衡因子为 f ，则一棵 AVL 树的任意节点的平衡因子皆满足 −1≤f≤1 。

节点的平衡因子（balance factor）定义为节点左子树的高度减去右子树的高度，同时规定空节点的平衡因子为 0 。我们同样将获取节点平衡因子的功能封装成函数，方便后续使用：

1
2
3
4
5
6
7
8
9
/* 获取平衡因子 */
int balanceFactor(TreeNode *node) {
    // 空节点平衡因子为 0
    if (node == NULL) {
        return 0;
    }
    // 节点平衡因子 = 左子树高度 - 右子树高度
    return height(node->left) - height(node->right);
}

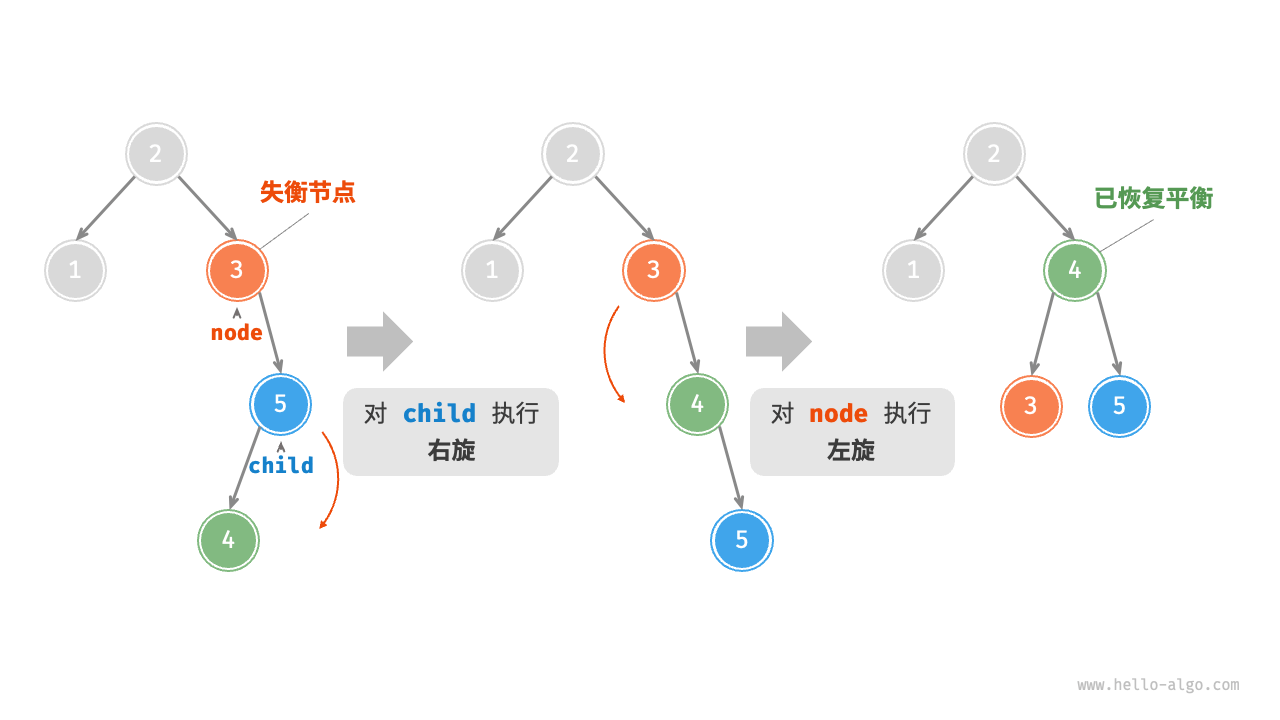
AVL树旋转

在不影响二叉树的中序遍历序列的前提下，使失衡节点重新恢复平衡。

将平衡因子绝对值 >1 的节点称为“失衡节点”。根据节点失衡情况的不同，旋转操作分为四种：右旋、左旋、先右旋后左旋、先左旋后右旋。

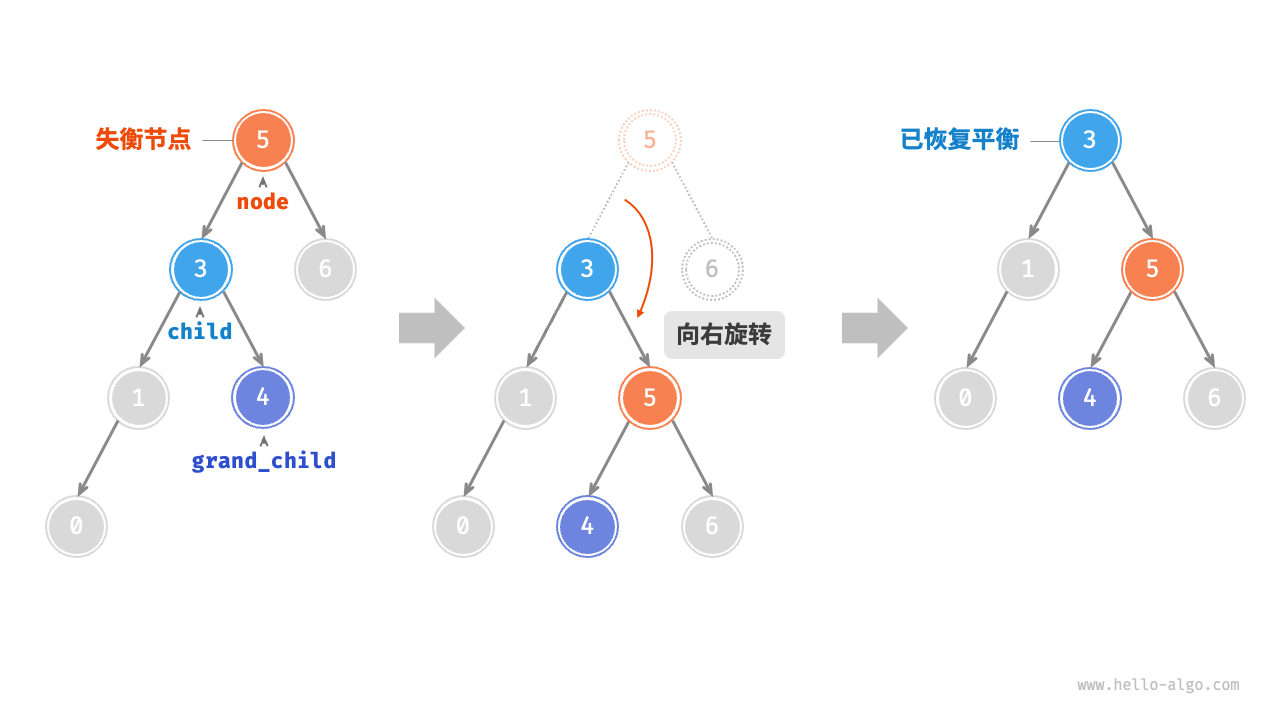
1、右旋

1732772213968

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/* 右旋操作 */
TreeNode *rightRotate(TreeNode *node) {
    TreeNode *child, *grandChild;
    child = node->left;
    grandChild = child->right;
    // 以 child 为原点，将 node 向右旋转
    child->right = node;
    node->left = grandChild;
    // 更新节点高度
    updateHeight(node);
    updateHeight(child);
    // 返回旋转后子树的根节点
    return child;
}

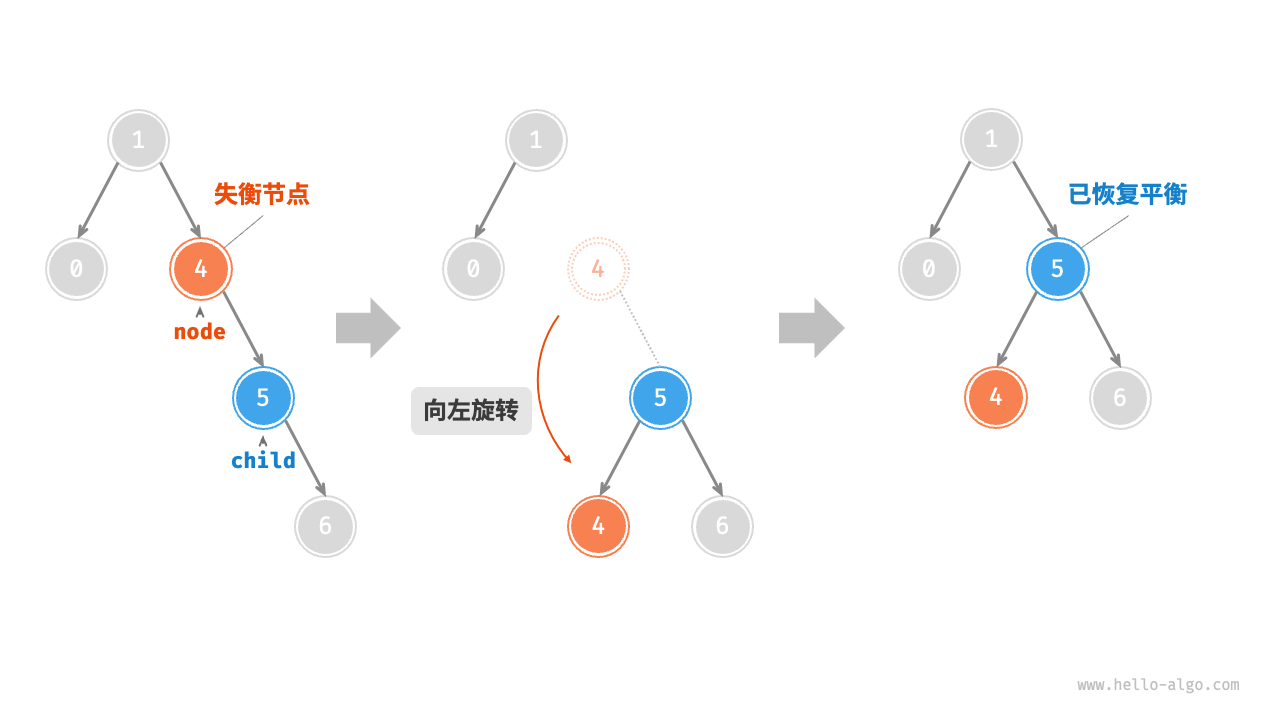
2、左旋

相应地考虑镜像

1732772294087

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/* 左旋操作 */
TreeNode *leftRotate(TreeNode *node) {
    TreeNode *child, *grandChild;
    child = node->right;
    grandChild = child->left;
    // 以 child 为原点，将 node 向左旋转
    child->left = node;
    node->right = grandChild;
    // 更新节点高度
    updateHeight(node);
    updateHeight(child);
    // 返回旋转后子树的根节点
    return child;
}

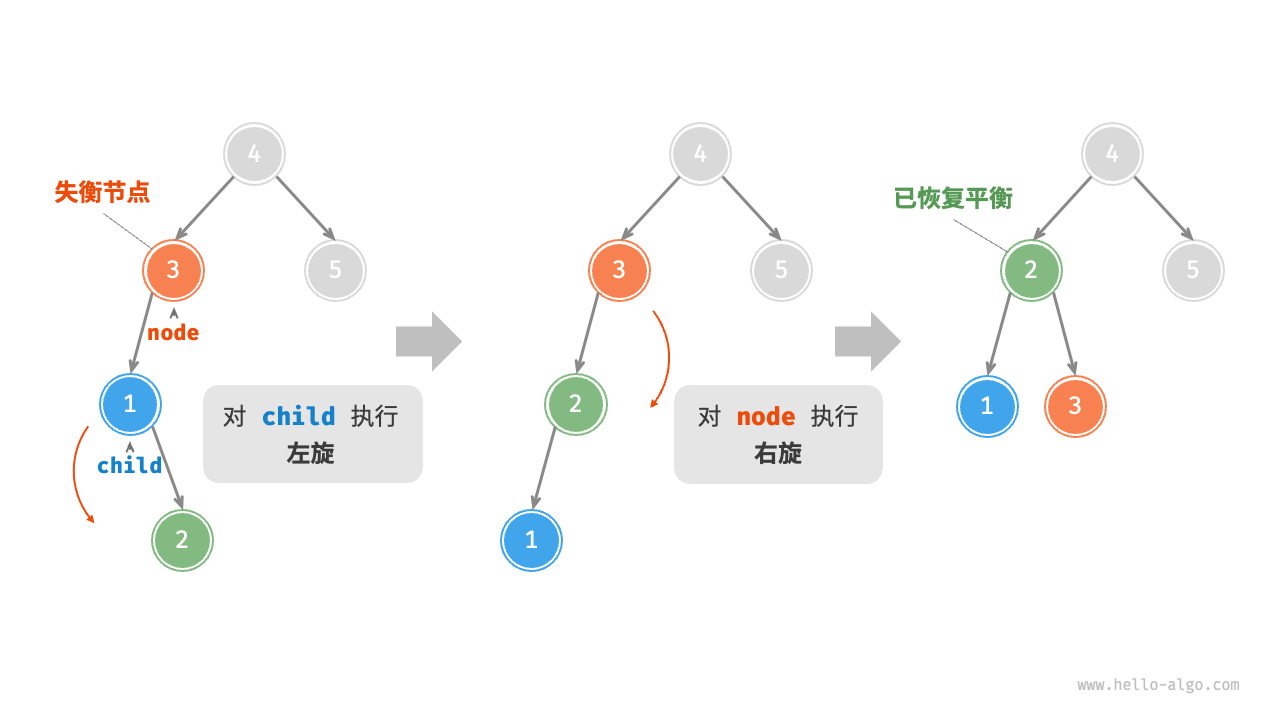
3、先左旋再右旋

1732772389673

4、先右旋后左旋

1732772496445

5、旋转选择

如下表所示，我们通过判断失衡节点的平衡因子以及较高一侧子节点的平衡因子的正负号，来确定失衡节点属于哪种情况

失衡节点的平衡因子 子节点的平衡因子 应采用的旋转方法
>1左偏树 >=0 右旋
>1左偏树 <0 先左旋后右旋
<-1右偏树 <=0 左旋
<-1右偏树 >0 先右旋后左旋

将以上规律封装成函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/* 执行旋转操作，使该子树重新恢复平衡 */
TreeNode *rotate(TreeNode *node) {
    // 获取节点 node 的平衡因子
    int bf = balanceFactor(node);
    // 左偏树
    if (bf > 1) {
        if (balanceFactor(node->left) >= 0) {
            // 右旋
            return rightRotate(node);
        } else {
            // 先左旋后右旋
            node->left = leftRotate(node->left);
            return rightRotate(node);
        }
    }
    // 右偏树
    if (bf < -1) {
        if (balanceFactor(node->right) <= 0) {
            // 左旋
            return leftRotate(node);
        } else {
            // 先右旋后左旋
            node->right = rightRotate(node->right);
            return leftRotate(node);
        }
    }
    // 平衡树，无须旋转，直接返回
    return node;
}

插入与删除操作

在 AVL 树中插入节点后，从该节点到根节点的路径上可能会出现一系列失衡节点。因此， 我们需要从这个节点开始，自底向上执行旋转操作，使所有失衡节点恢复平衡 。（递归形式恢复）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/* 插入节点 */
void insert(AVLTree *tree, int val) {
    tree->root = insertHelper(tree->root, val);
}

/* 递归插入节点（辅助函数） */
TreeNode *insertHelper(TreeNode *node, int val) {
    if (node == NULL) {
        return newTreeNode(val);
    }
    /* 1. 查找插入位置并插入节点 */
    if (val < node->val) {
        node->left = insertHelper(node->left, val);
    } else if (val > node->val) {
        node->right = insertHelper(node->right, val);
    } else {
        // 重复节点不插入，直接返回
        return node;
    }
    // 更新节点高度
    updateHeight(node);
    /* 2. 执行旋转操作，使该子树重新恢复平衡 */
    node = rotate(node);
    // 返回子树的根节点
    return node;
}

删除同理，也是从底至顶地进行旋转操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
/* 删除节点 */
// 由于引入了 stdio.h ，此处无法使用 remove 关键词
void removeItem(AVLTree *tree, int val) {
    TreeNode *root = removeHelper(tree->root, val);
}

/* 递归删除节点（辅助函数） */
TreeNode *removeHelper(TreeNode *node, int val) {
    TreeNode *child, *grandChild;
    if (node == NULL) {
        return NULL;
    }
    /* 1. 查找节点并删除 */
    if (val < node->val) {
        node->left = removeHelper(node->left, val);
    } else if (val > node->val) {
        node->right = removeHelper(node->right, val);
    } else {
        if (node->left == NULL || node->right == NULL) {
            child = node->left;
            if (node->right != NULL) {
                child = node->right;
            }
            // 子节点数量 = 0 ，直接删除 node 并返回
            if (child == NULL) {
                return NULL;
            } else {
                // 子节点数量 = 1 ，直接删除 node
                node = child;
            }
        } else {
            // 子节点数量 = 2 ，则将中序遍历的下个节点删除，并用该节点替换当前节点
            TreeNode *temp = node->right;
            while (temp->left != NULL) {
                temp = temp->left;
            }
            int tempVal = temp->val;
            node->right = removeHelper(node->right, temp->val);
            node->val = tempVal;
        }
    }
    // 更新节点高度
    updateHeight(node);
    /* 2. 执行旋转操作，使该子树重新恢复平衡 */
    node = rotate(node);
    // 返回子树的根节点
    return node;
}

红黑树

红黑树是一种特化的AVL树（平衡二叉树），都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能

它的左右子树高差有可能大于1，所以红黑树不是严格意义上的平衡二叉树（AVL），但对之进行平衡的代价较低， 其平均统计性能要强于 AVL

特征

红黑树是每个节点都带有颜色属性的二叉查找树，颜色或红色或黑色

  1. 根节点是黑色
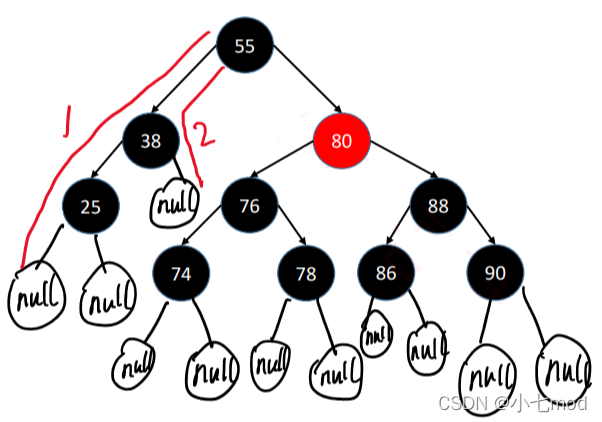
  2. 叶子节点（外部节点，空节点）都是 黑色， 这里的叶子节点指的是最底层的空节点（外部节点），下图中的那些null节点才是叶子节点，null节点的父节点在红黑树里不将其看作叶子节点
  3. 每个红色节点的两个子节点都是黑色（从每个叶子到根的所有路径上不能有两个连续的红色节点）
  4. 每个红色结点的父节点都是黑色
  5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点
  6. 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长

红黑树因而近似平衡（最短路径就是全黑节点，最长路径就是一个红节点一个黑节点，当从根节点到叶子节点的路径上黑色节点相同时，最长路径刚好是最短路径的两倍）

真正被定义为叶子结点的是那些空结点

1732774029129

查找操作时，它和普通的相对平衡的二叉搜索树的效率相同，都是通过相同的方式来查找的，没有用到红黑树特有的特性。

但如果插入的时候是有序数据，那么红黑树的查询效率就比二叉搜索树要高了，因为此时二叉搜索树不是平衡树，它的时间复杂度O(N)。

插入和删除操作

插入和删除操作时，由于红黑树的每次操作平均要旋转一次和变换颜色，所以它比普通的二叉搜索树效率要低一点，不过时间复杂度仍然是O(logN)。总之，红黑树的优点就是对有序数据的查询操作不会慢到O(logN)的时间复杂度。

插入时将插入的结点设置为红色，只需要考虑连续红色的情况

总结

利用对树中的结点“红黑着色”的要求，降低了平衡性的条件，达到局部平衡，有着良好的最坏情况运行时间，它可以在O(log n)时间内做查找，插入和删除，这里的n是树中元素的数目。

B-树

B 树（B-tree）是一种自平衡的搜索树，能够保持数据有序。这种数据结构能够让查找数据、顺序访问、插入数据及删除的动作，都在对数时间内完成。B 树的每个节点可以拥有两个以上的子节点，因此 B 树是一种多路搜索树。

在 B 树中，有两种节点：

  1. 内部节点（internal node）：存储了数据以及指向其子节点的指针。
  2. 叶子节点（leaf node）：与内部节点不同的是，叶子节点只存储数据，并没有子节点。

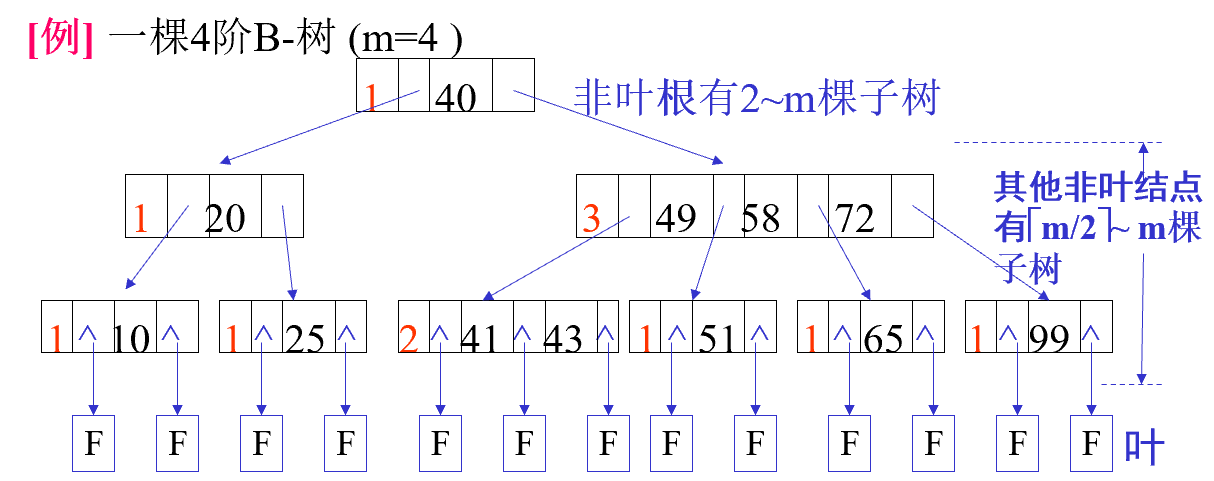
性质

一棵 m 阶的 B 树满足的性质如下：

  1. 树中每个结点最多有m棵子树
  2. 若根结点不是叶子结点，则最少有两棵子树
  3. 除根之外的所有非叶子结点最少有[m/2]棵子树
  4. 所有非叶子结点包含 （n,A0,K1,A1,K2,…,Kn,An）信息数据；其中n为结点中关键字个数，Ai为指向子树的指针，Ki为关键字
  5. 所有叶子结点在同一层上，且不带信息

1732778419794

每个结点的结构为：（n，A0，K1，A1，K2，A2，… ，Kn，An）

其中，Ki(1≤i≤n)为关键字，且Ki<Ki+1(1≤i≤n-1)。

Ai(0≤i≤n)为指向子树根结点的指针。

且Ai所指子树所有结点中的关键字均小于Ki+1。

n为结点中关键字的个数，满足ceil(m/2)-1≤n≤m-1。

1732779390638

结构定义

1
2
3
4
5
6
7
8
9
10
B-树节点定义
#define m 3 //B-树的阶
typedef struct BTNode {
  int keynum;    //关键字个数
  struct BTNode *parent;     //双亲指针
  KeyType key[m+1];          //0号未用，关键字数组 
  struct BTNode *ptr[m+1];   //0号未用，子树指针数组
  Record *recptr[m+1];       //0号未用，磁盘记录地址数组
} BTNode, *BTree;

查找

  1. 在当前结点*p中顺序或者折半查找若找到某个i，满足key[i]=K，则查找成功，返回p、i、1；
    否则，确定满足key[i]<K<key[i+1]的i值
  2. 若*p结点中的ptr[i]为空指针，则查找失败，返回p、i、0
  3. 从磁盘上读入ptr[i]指示的结点 DiskRead(p->ptr[i])，将此结点作为当前结点，转(1）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Result SearchBTree(BTree T, KeyType K)
{   
  p = T; q = NULL; found = FALSE; i=0;//q指向p的双亲
  while (p && ! found) 
  {
    i = Search(p, K); //在p->key[1..keynum]中找i, 
                      // 使得key[i]<=K<key[i+1]
    if( i>0 && p->key[i]==K )
      found = TRUE;
    else 
    { 
      q = p;
      p = p->ptr[i];   
    }
  }
  if (found)
    return (p,i,1);
  else
    return (q,i,0);
}//SearchBTree

插入

  1. 如果叶子节点空间足够，即该节点的关键字数小于 m-1，则直接插入在叶子节点的左边或右边；

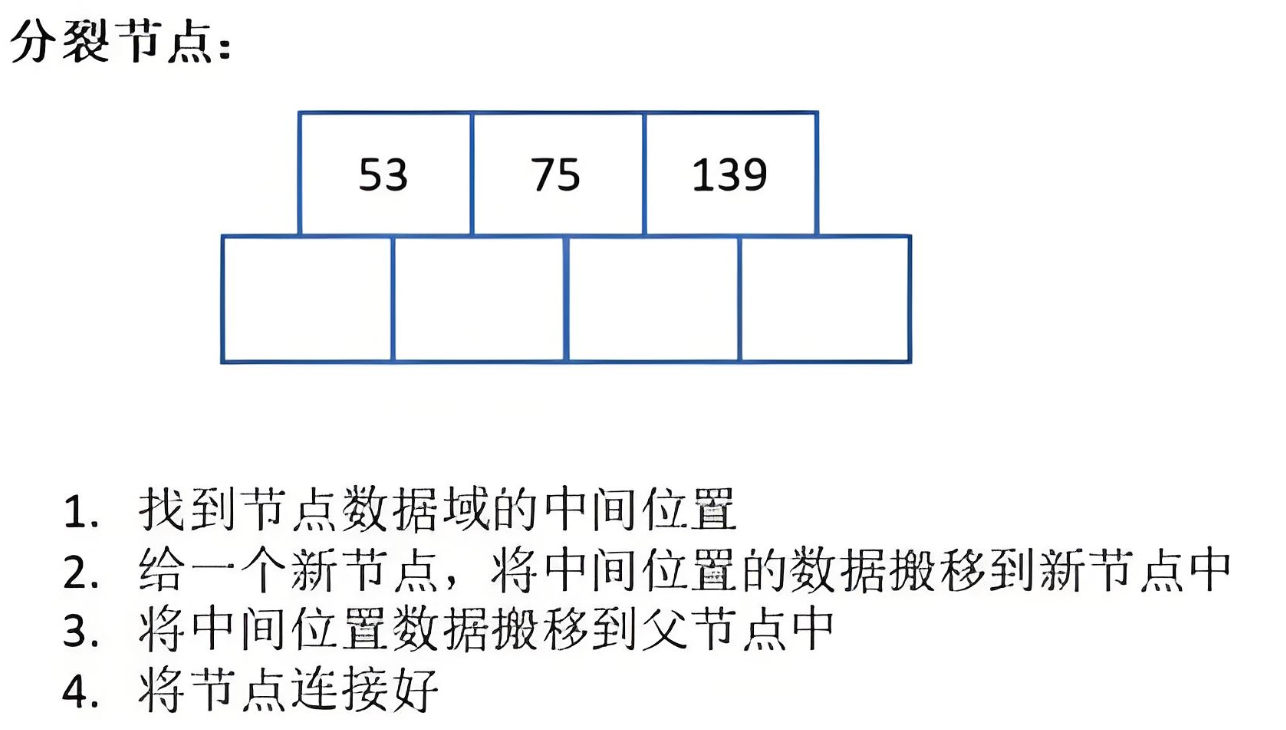
  2. 如果空间满了以至于没有足够的空间去添加新的元素，即该节点的关键字数已经有了 m个，则需要将该节点进行「分裂」，将一半数量的关键字元素分裂到新的其相邻右节点中，中间关键字元素上移到父节点中，而且当节点中关键元素向右移动了，相关的指针也需要向右移。

    1. 从该节点的原有元素和新的元素中选择出中位数
    2. 小于这一中位数的元素放入左边节点，大于这一中位数的元素放入右边节点，中位数作为分隔值。
    3. 分隔值被插入到父节点中，这可能会造成父节点分裂，分裂父节点时可能又会使它的父节点分裂，以此类推。如果没有父节点（这一节点是根节点），就创建一个新的根节点（增加了树的高度）。

如果一直分裂到根节点，那么就需要创建一个新的根节点。它有一个分隔值和两个子节点。

第一个关键字的插入也是从空树开始。

1732781098225

1732781140254

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
void BTree::insert(int k) {
  // 如果树为空树
  if (root == NULL) {
    // 为根节点分配空间
    root = new BTreeNode(t, true);
    root->keys[0] = k;  // 插入节点 k
    root->n = 1;        // 更新根节点的关键字的个数为 1
  } else {
    // 当根节点已满，则对B-树进行生长操作
    if (root->n == 2 * t - 1) {
      // 为新的根节点分配空间
      BTreeNode *s = new BTreeNode(t, false);

      // 将旧的根节点作为新的根节点的孩子
      s->C[0] = root;

      // 将旧的根节点分裂为两个，并将一个关键字上移到新的根节点
      s->splitChild(0, root);

      // 新的根节点有两个孩子节点
      // 确定哪一个孩子将拥有新插入的关键字
      int i = 0;
      if (s->keys[0] < k) i++;
      s->C[i]->insertNonFull(k);

      // 新的根节点更新为 s
      root = s;
    } else  // 根节点未满，调用 insertNonFull() 函数进行插入
      root->insertNonFull(k);
  }
}

// 将关键字 k 插入到一个未满的节点中
void BTreeNode::insertNonFull(int k) {
  // 初始化 i 为节点中的最后一个关键字的位置
  int i = n - 1;

  // 如果当前节点是叶子节点
  if (leaf == true) {
    // 下面的循环做两件事：
    // a) 找到新插入的关键字位置并插入
    // b) 移动所有大于关键字 k 的向后移动一个位置
    while (i >= 0 && keys[i] > k) {
      keys[i + 1] = keys[i];
      i--;
    }

    // 插入新的关键字，节点包含的关键字个数加 1
    keys[i + 1] = k;
    n = n + 1;
  } else {
    // 找到第一个大于关键字 k 的关键字 keys[i] 的孩子节点
    while (i >= 0 && keys[i] > k) i--;

    // 检查孩子节点是否已满
    if (C[i + 1]->n == 2 * t - 1) {
      // 如果已满，则进行分裂操作
      splitChild(i + 1, C[i + 1]);

      // 分裂后，C[i] 中间的关键字上移到父节点，
      // C[i] 分裂称为两个孩子节点
      // 找到新插入关键字应该插入的节点位置
      if (keys[i + 1] < k) i++;
    }
    C[i + 1]->insertNonFull(k);
  }
}

// 节点 y 已满，则分裂节点 y
void BTreeNode::splitChild(int i, BTreeNode *y) {
  // 创建一个新的节点存储 t - 1 个关键字
  BTreeNode *z = new BTreeNode(y->t, y->leaf);
  z->n = t - 1;

  // 将节点 y 的后 t -1 个关键字拷贝到 z 中
  for (int j = 0; j < t - 1; j++) z->keys[j] = y->keys[j + t];

  // 如果 y 不是叶子节点，拷贝 y 的后 t 个孩子节点到 z中
  if (y->leaf == false) {
    for (int j = 0; j < t; j++) z->C[j] = y->C[j + t];
  }

  // 将 y 所包含的关键字的个数设置为 t -1
  // 因为已满则为2t -1 ，节点 z 中包含 t - 1 个
  // 一个关键字需要上移
  // 所以 y 中包含的关键字变为 2t-1 - (t-1) -1
  y->n = t - 1;

  // 给当前节点的指针分配新的空间，
  // 因为有新的关键字加入，父节点将多一个孩子。
  for (int j = n; j >= i + 1; j--) C[j + 1] = C[j];

  // 当前节点的下一个孩子设置为z
  C[i + 1] = z;

  // 将所有父节点中比上移的关键字大的关键字后移
  // 找到上移节点的关键字的位置
  for (int j = n - 1; j >= i; j--) keys[j + 1] = keys[j];

  // 拷贝 y 的中间关键字到其父节点中
  keys[i] = y->keys[t - 1];

  // 当前节点包含的关键字个数加 1
  n = n + 1;
}

写不下去了参考这个吧Btree

B+树

B+树是B树的变形，是在B树基础上优化的多路平衡搜索树

B+树是一种多叉排序树，即每个节点通常有多个孩子。一棵 B+ 树包含根节点、内部节点和叶子节点。根节点可能是一个叶子节点，也可能是一个包含两个或两个以上孩子节点的节点。
B+ 树的特点是能够保持数据稳定有序，其插入与修改拥有较稳定的对数时间复杂度。B+树元素自
底向上插入，这与二叉树恰好相反。
首先介绍一棵 m 阶 B+ 树的特性。m 表示这个树的每一个节点最多可以拥有的子节点个数。一棵
m 阶的 B+ 树和 B 树的差异在于:

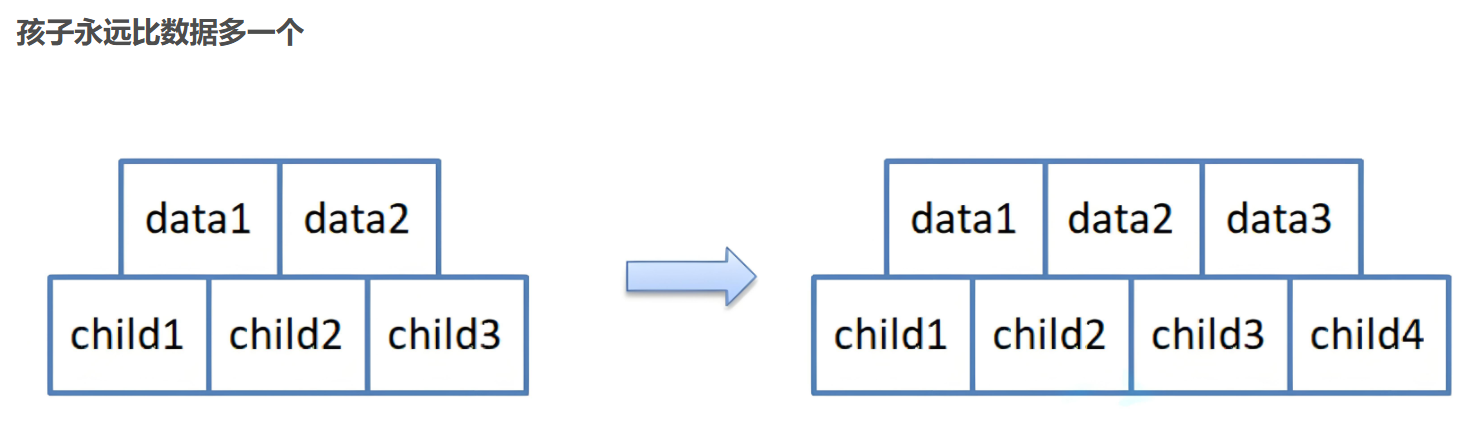
  1. 有n棵子树的节点中含有n-1个关键字(即将区间分为n-1个子区间，每个子区间对应一棵子树)\
  2. 所有叶子节点中包含了全部关键字的信息，及指向含这些关键字记录的指针，且叶子节点本身依关键字的大小自小而大顺序链接。
  3. 所有的非叶子节点可以看成是索引部分，节点中仅含有其子树(根节点)中的最大(或最小)关键字。
  4. 除根节点外，其他所有节点中所含关键字的个数最少有「n/2](注意:B 树中除根以外的所有非叶子节点至少有[n/2]棵子树)
  5. 分支节点的子树指针与关键字个数相同
  6. 分支节点的子树指针p[i]指向关键字值大小在[k[i]，k[i+1])区间之间
  7. 所有叶子节点增加一个链接指针链接在一起
  8. 所有关键字及其映射数据都在叶子节点出现

同时，B+ 树为了方便范围查询，叶子节点之间还用指针串联起来。

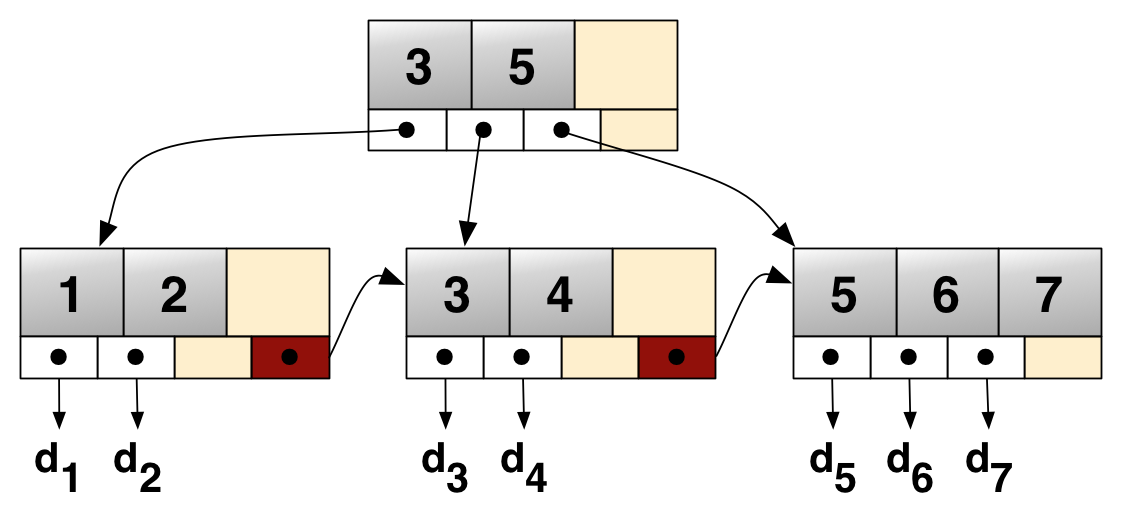
以下是一棵 B+ 树的典型结构：

1732806145671

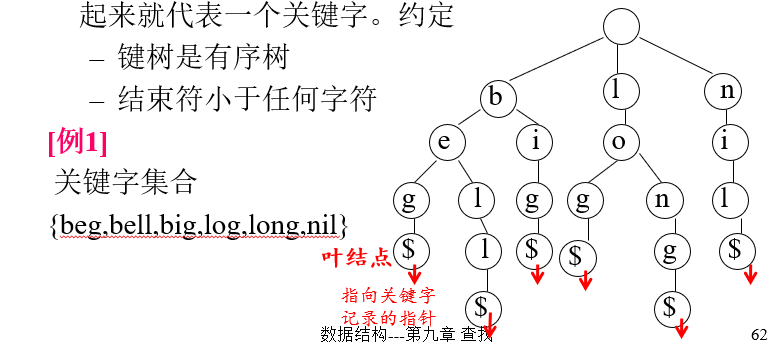
键树

将关键字分解为字符的多叉树

多叉树中的每个结点只代表关键字中的一个字符

叶结点用于表示字符串的结束符(如‘$’)，并含有指向该关键字记录的指针。

而从根到叶子的路径上所有的结点对应的字符连接起来就代表一个关键字。

1732888070053

键树的存储结构及其操作

1732889192518

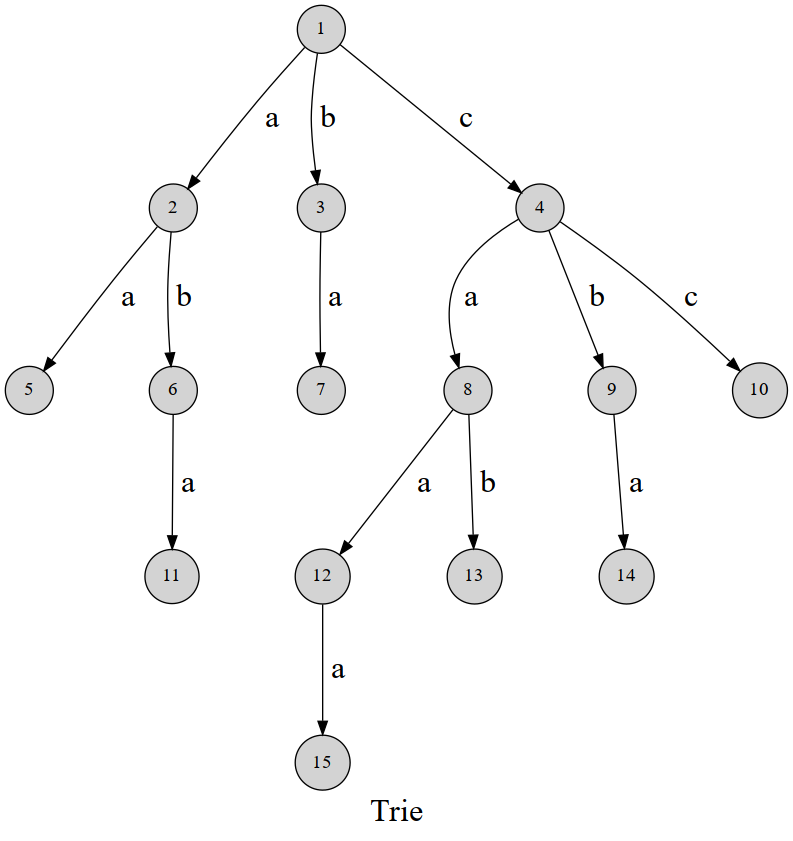
Trie树（字典树）

1732889792976

若从键树中某个结点开始到叶子结点的路径上的每个结点中都只有一个孩子，则将该路径上的所有结点压缩成一个“叶子结点”，且叶子结点中存储有指向记录的指针。

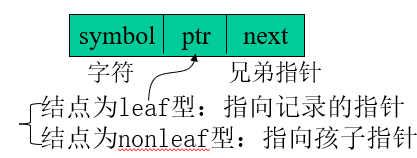
分支结点：num—有用指针的数量

ptr[0..m]—指针数组

叶子结点：key—关键字

recptr—指向对应记录的指针

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
struct trie {
  int nex[100000][26], cnt;
  bool exist[100000];  // 该结点结尾的字符串是否存在

  void insert(char *s, int l) {  // 插入字符串
    int p = 0;
    for (int i = 0; i < l; i++) {
      int c = s[i] - 'a';
      if (!nex[p][c]) nex[p][c] = ++cnt;  // 如果没有，就添加结点
      p = nex[p][c];
    }
    exist[p] = true;
  }

  bool find(char *s, int l) {  // 查找字符串
    int p = 0;
    for (int i = 0; i < l; i++) {
      int c = s[i] - 'a';
      if (!nex[p][c]) return 0;
      p = nex[p][c];
    }
    return exist[p];
  }
};
  • Title: 动态查找表
  • Author: time will tell
  • Created at : 2024-11-28 09:11:59
  • Updated at : 2024-12-12 15:36:40
  • Link: https://sbwrn.github.io/2024/11/28/动态查找表/
  • License: This work is licensed under CC BY-NC-SA 4.0.
Comments
On this page
动态查找表
  1. 1. 动态查找表
    1. 1.1. 二叉排序树BST
      1. 1.1.0.1. 定义
    2. 1.1.1. 操作
      1. 1.1.1.1. 查找
      2. 1.1.1.2. 插入
      3. 1.1.1.3. 删除
  2. 1.2. 平衡二叉树（AVL树）
    1. 1.2.0.1. 定义
  3. 1.2.1. 查找的分析
  4. 1.2.2. 结点的存储结构
  5. 1.2.3. 平衡二叉树上的操作
    1. 1.2.3.1. 1、结点高度
    2. 1.2.3.2. 2、结点平衡因子
  6. 1.2.4. AVL树旋转
    1. 1.2.4.1. 1、右旋
    2. 1.2.4.2. 2、左旋
    3. 1.2.4.3. 3、先左旋再右旋
    4. 1.2.4.4. 4、先右旋后左旋
    5. 1.2.4.5. 5、旋转选择
  7. 1.2.5. 插入与删除操作
  • 1.3. 红黑树
    1. 1.3.1. 特征
    2. 1.3.2. 插入和删除操作
    3. 1.3.3. 总结
  • 1.4. B-树
    1. 1.4.1. 性质
    2. 1.4.2. 结构定义
    3. 1.4.3. 查找
    4. 1.4.4. 插入
  • 1.5. B+树
  • 1.6. 键树
    1. 1.6.1. 键树的存储结构及其操作
  • 1.7. Trie树（字典树）