哈夫曼树

time will tell Lv4
  2024-11-16 10:48:33 2024-11-16 10:48:33 Created   2024-11-16 17:34:42 2024-11-16 17:34:42 Updated      

赫夫曼树（最优二叉树）

引入

1、搜索树/比较树的效率和数据有关系

2、可以根据数据来生成高效的树

3、高效的树，是和树的深度有关的

结点权值 : 和叶子结点对应的一个有某种意义的实数(Wi)

树的路径长度 : 从树根到每一个结点的路径上的分支数之和。

带权路径长度 : 叶子结点的路径长度与该结点的权之积。

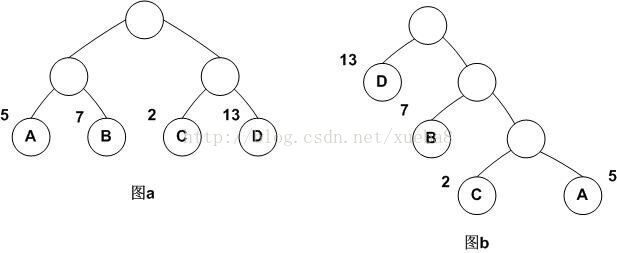
1731581076811

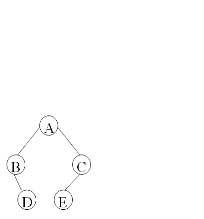
图a： WPL=52+72+22+132=54

图b： WPL=53+23+72+131=48

树的带权路径长度 : 树中所有叶子结点的带权路径长度之和。

1731316693654

那么根据定义，

最优二叉树(Huffman，赫夫曼/哈夫曼/霍夫曼树) :带权路径长度WPL最小的二叉树。

赫夫曼算法：构造最优二叉树

[基本思想]使权大的结点靠近根

[算法思路]

(1)将给定权值从小到大排序成{w1,w2,…,wm}，生成一个森林F={T1,T2,…,Tm}，其中Ti是一个带权Wi的根结点，它的左右子树均空。

(2)把F中根的权值最小的两棵二叉树T1和T2合并成一棵新的二叉树T： T的左子树是T1，右子树是T2，T的根的权值是T1、T2树根结点权值之和。

(3)将T按权值大小加入F中，同时从F中删去T1和T2

(4)重复(2)和(3)，直到F中只含一棵树为止，该树即为所求。

[操作要点]对权值的合并、删除与替换，总是合并当前值最小的两个

赫夫曼树的存储结构

赫夫曼树构造过程决定了没有度为1的节点。

由性质3：n0=n2+1，得到全部结点数为2n-1个

顺序存储

用大小为2n的向量存储赫夫曼树—顺序存储

1
2
3
4
5
6
7
typedef struct {
    unsigned int  weight;
    unsigned int  parent, lchild, rchild;
}HTNode, *HuffmanTree; 
//在数组中构造链式关系，便于从叶节点构造到根
//采用动态分配存储空间方式构造一个数组方式的存储

构造算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
bool BuildHT(HuffmanTree &HT, int *w, int n)
// w存放n个叶结点的权值(均>0)，构造赫夫曼树HT
{ if  ( n<=1 )  { HT=NULL; return false; }
  m=2*n-1;    //计算总结点个数
  HT=(HuffmanTree)malloc((m+1)sizeof(HTNode));
  if(!HT) return false;
 //初始化HT
  for (p=HT+1, i=1; i<=n; ++i, ++p, ++w)  //前n个有权重
    *p={*w,0,0,0}; 
  for (; i<=m; ++i, ++p)  //后n-1个无权重，待合并结点时填上
    *p={0,0,0,0};
  for (i=n+1; i<=m; ++i) {   //建赫夫曼树
    Select(HT, i-1, s1, s2); 
    //在HT[1..i-1]中选择parent为0且权值最小的两个结点
    HT[s1].parent=i; HT[s2].parent=i; 
    HT[i].lchild=s1; HT[i].rchild=s2;
    HT[i].weight=HT[s1].weight+HT[s2].weight;
  }
  return true;
}//BuildHT


虽然在赫夫曼树的构造中有说明要删除已经合成过的子树，但这对于算法要求显然不可能。实际操作中，我们会尝试创建一个2*n+1大小的数组来存储初始数组，并将后续生成的树放入数组中从而省略删除子树的过程，而通过parent是否为空结点来判断子树是否被合并过。

因此完整的构造算法应该如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
bool Build(HuffmanTree &HT,int * w,int n)
{
    if(n < 1)
        return false;
    int m = 2 * n - 1;
    HT = (HuffmanTree)malloc(m * sizeof(HTNode));
    if(!HT)
        return false;
    for(int i = 0; i < n; i++)
    {
        HT[i].weight = w[i];
        HT[i].parent = -1;
        HT[i].lchild = -1;
        HT[i].rchild = -1;
    }
    for(int i = n; i <= m; i++)
    {
        HT[i].weight = -1;
        HT[i].parent = -1;
        HT[i].lchild = -1;
        HT[i].rchild = -1;
    }
    for(int i = n;i<m;i++)
    {
        int s1,s2;
        Select(HT,i,s1,s2);
        HT[s1].parent = i,HT[s2].parent = i;
        HT[i].lchild = s1,HT[i].rchild = s2;
        HT[i].weight = HT[s1].weight + HT[s2].weight;
    }
    return true;

}

其中 select 函数的功能是从0~(i-1)的下标中选择两个权重最小的数，并返回他们的下标。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
bool Select(HuffmanTree &HT,int n,int &s1,int &s2)
{
    int m = 0;
    for(int i = 0; i < n; i++)
    {
        if(HT[i].parent == -1)
        {
            m = i;
            break;
        }
    }
    for(int i = 0; i < n; i++)
    {
        if(HT[i].parent == -1 && HT[i].weight < HT[m].weight)
            m = i;
    }
    s1 = m;
    for(int i = 0; i < n; i++)
    {
        if(HT[i].parent == -1 && i != s1)
        {
            m = i;
            break;
        }
    }
    for(int i = 0;i < n;i++)
    {
        if(HT[i].parent == -1 && i != s1 && HT[i].weight < HT[m].weight)
            m = i;
    }
    s2 = m;
    return true;
}

赫夫曼编码

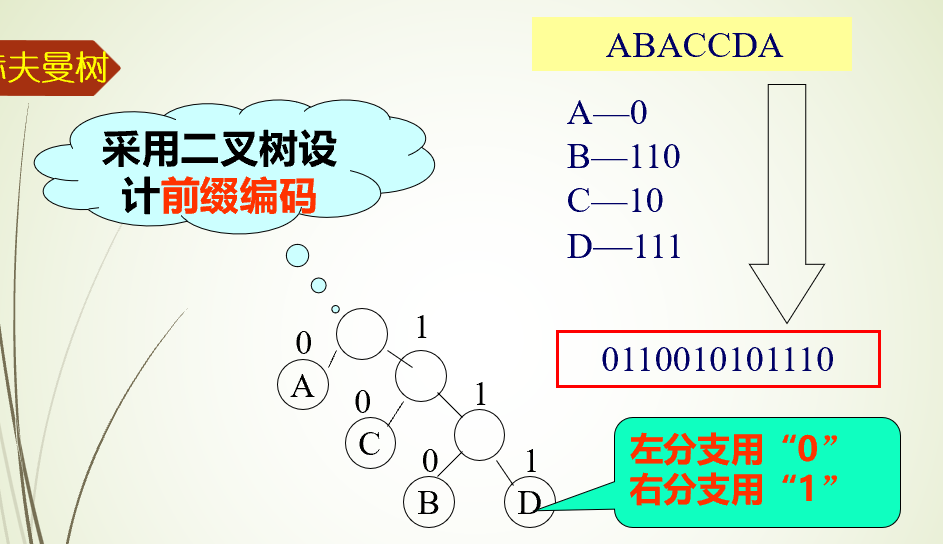
前缀编码

任一字符的编码都不是另一个字符的编码的前缀－前缀编码

特点：

赫夫曼编码是不等长编码

赫夫曼编码是前缀编码，即任一字符的编码都不是另一字符编码的前缀

赫夫曼编码树中没有度为1的结点。若叶子结点的个数为n，则赫夫曼编码树的结点总数为2n-1

发送过程：根据由赫夫曼树得到的编码表送出字符数据

接收过程：按左0、右1的规定，从根结点走到一个叶结点，完成一个字符的译码。反复此过程，直到接收数据结束

译码过程：

规定赫夫曼树中的左分支代表0，右分支代表1，则从根结点到每个叶结点所经过的路径分支组成的0和1的序列便为该结点对应字符的编码

分解接收字符串：遇“0”向左，遇“1”向右；一旦到达叶子结点，则译出一个字符，反复由根出发，直到译码完成。

1731317974186

使用类似赫夫曼树的存储结构，频率最高的字符在最靠近根结点的地方，做到最大程度上减少编码开销

赫夫曼编码码表构造

主数据结构：赫夫曼树HT

赫夫曼编码表HC

辅助数据结构：cd {编码工作空间}

1731318981612

依次求叶子HT[i]的编码HC[i]，i=1..n

1)置cd中记录编码位置的初值：start=n-1;

置上溯的起点：c=i;

取c的父结点：f=HT[c].parent;

2)根据HT，c、f上溯直到根结点(f=0)，依次产生的编码(c是f的左孩子编码为0；否则为1)置入cd的相应编码空间cd[start-1]并调整 start(减1)

3)为第i个字符编码申请（n-start）大小的字符空间HC[i]，cd复制

给HC[i]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void  HuffmanCoding(HuffmanTree HT, int n, HuffmanCode &HC)
// 求赫夫曼树HT的n个字符的赫夫曼编码HC
{ 
  HC=(HuffmanCode)malloc((n+1)sizeof(char *));
  cd=(char *) malloc(n*sizeof(char)) ;  //分配编码的工作空间
  cd[n-1]=0 ;
  for (i=1; i<=n; ++i){   //为每个字符求编码
    start=n-1;
    for (c=i, f=HT[i].parent; f!=0; c=f, f=HT[f].parent ) {
      if(HT[f].lchild==c) cd[--start]='0';
      else cd[--start]='1';
    }
    HC[i]= (char *)malloc((n-start)*sizeof(char));
    strcpy(HC[i], &cd[start]);
  }
  free(cd); 
}//HuffmanCoding

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
#include<stdlib.h>
#include<stdio.h>
/*哈夫曼树结构*/
//可以用数组连续存储，不会浪费空间
//故用数组下标存储左右孩子、父亲结点
typedef struct
{
	int weight;
	int left;
	int right;
	int parent;
}Node, * HuffmanTree;
 
//存储哈夫曼编码
typedef char* HuffmanCode;
void CreateHuffmanTree(HuffmanTree* T, int w[], int n);
void select(HuffmanTree* T, int n, int* m1, int* m2);
void CreateHuffmanCode(HuffmanTree* T, HuffmanCode* C, int n);
/*创建哈夫曼树*/
//传入n个权重，作为哈夫曼树的n个叶子结点
void CreateHuffmanTree(HuffmanTree* T, int w[], int n)
{
	int m = 2 * n - 1;//n个叶子结点，共m个结点
	int m1, m2;//用于建立下一个结点的两结点，值为最小的两个
	*T = (HuffmanTree)malloc((m + 1) * sizeof(Node));
	//初始化前n个结点（叶子结点），权重赋值，暂时没有左右孩子与父亲
	for (int i = 1; i <= n; i++)
	{
		(*T)[i].weight = w[i];
		(*T)[i].left = 0;
		(*T)[i].right = 0;
		(*T)[i].parent = 0;
	}
 
	//初始化[n+1,m]个结点(非叶子结点)
	for (int i = n + 1; i <= m; i++)
	{
		(*T)[i].weight = 0;
		(*T)[i].left = 0;
		(*T)[i].right = 0;
		(*T)[i].parent = 0;
	}
 
	//开始建树，第i个结点的两孩子为m1,m2，权重为两孩子结点权重之和
	for (int i = n + 1; i <= m; i++)
	{
		select(T, i - 1, &m1, &m2);
		(*T)[i].left = m1;
		(*T)[i].right = m2;
		(*T)[m1].parent = i;
		(*T)[m2].parent = i;
		(*T)[i].weight = (*T)[m1].weight + (*T)[m2].weight;
 
		printf("%d (%d %d)\n", (*T)[i].weight, (*T)[m1].weight, (*T)[m2].weight);
	}
	printf("\n");
}
 
/*选取得到n个无父节点的两最小结点*/
void select(HuffmanTree* T, int n, int* m1, int* m2)
{
	int m;//存储最小值的数组下标
 
	//给m赋初值
	for (int i = 1; i <= n; i++)
	{
		if ((*T)[i].parent == 0)
		{
			m = i;
			break;
		}
	}
	//找到当前最小的权重（叶子结点）
	for (int i = 1; i <= n; i++)
	{
		if ((*T)[i].parent == 0 && (*T)[i].weight < (*T)[m].weight)
		{
			m = i;
		}
	}
	//先赋给m1保存一个，再去寻找第二小的值
	*m1 = m;
	for (int i = 1; i <= n; i++)
	{
		if ((*T)[i].parent == 0 && i != *m1)
		{
			m = i;
			break;
		}
	}
	for (int i = 1; i <= n; i++)
	{
		if ((*T)[i].parent == 0 && i != *m1 && (*T)[i].weight < (*T)[m].weight)
		{
			m = i;
		}
	}
	//保存第二小的数
	*m2 = m;
}
 
/*创建哈夫曼编码*/
//从n个叶子结点到根节点逆向求解
void CreateHuffmanCode(HuffmanTree* T, HuffmanCode* C, int n)
{
	//编码长度为s-1,第s位为\0
	int s = n - 1;
	//当前结点的父节点数组下标
	int p = 0;
	//为哈夫曼编码分配空间
	C = (HuffmanCode*)malloc((n + 1) * sizeof(char*));
	//临时保存当前叶子结点的哈夫曼编码
	char* cd = (char*)malloc(n * sizeof(char));
	//最后一位为\0
	cd[n - 1] = '\0';
 
	for (int i = 1; i <= n; i++)
	{
		s = n - 1;
		//c指向当前结点,p指向此结点的父节点,两者交替上升，直到根节点
		for (int c = i, p = (*T)[i].parent; p != 0; c = p, p = (*T)[p].parent)
		{
			//判断此结点为父节点的左孩子还是右孩子
			if ((*T)[p].left == c)
				cd[--s] = '0';//左孩子就是编码0
			else
				cd[--s] = '1';//右孩子就是编码1
		}
		//为第i个编码分配空间
		C[i] = (char*)malloc((n - s) * sizeof(char));
		//将此编码赋值到整体编码中
		strcpy(C[i], &cd[s]);
	}
	//释放
	free(cd);
	//打印编码序列
	for (int i = 1; i <= n; i++)
	{
		printf("%d %s", (*T)[i].weight, C[i]);
		printf("\n");
	}
}
 
int main()
{
	HuffmanTree T;
	HuffmanCode C;
	int n, w1, * w;
	scanf_s("%d", &n);
	w = (int*)malloc((n + 1) * sizeof(int));
	for (int i = 1; i <= n; i++)
	{
		scanf_s("%d", &w1);
		w[i] = w1;
	}
	printf("\n");
	CreateHuffmanTree(&T, w, n);
	CreateHuffmanCode(&T, &C, n);
	return 0;
}

线索二叉树

普通二叉树存在以下问题

  • 在n个结点的二叉树中，必定有n+1个空链域（叶子结点的左右子树空间浪费了）
  • 二叉树的遍历，无论是递归还是非递归算法，效率都不算高。

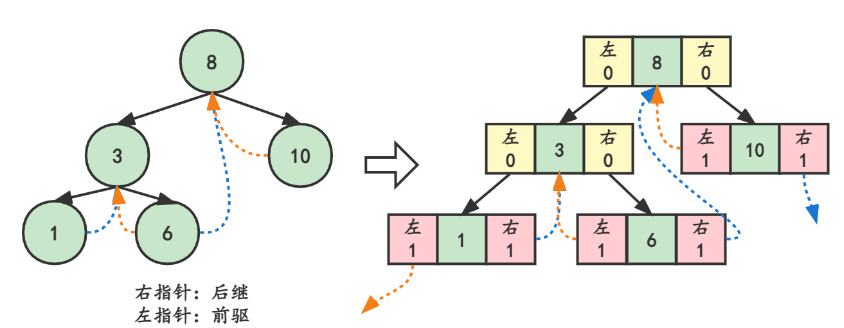
利用二叉链表的空指针域，建立指向该结点的前驱/后继(某种遍历方式下)结点的指针，方便二叉树的线性化使用。(n个结点的二叉树含有n+1空指针域)

在建立二叉树 的同时记录下前驱后继的关系，这样我们在寻找前驱后继结点时的效率将会大大提升

线索化

  • 若结点的左子树为空，则该结点的左孩子指针指向其前驱结点
  • 若结点的右子树为空，则该结点的右孩子指针指向其后继结点

这种指向前驱和后继的指针称为 线索 ，将一棵普通的二叉树以某种次序遍历，并添加线索的过程称为线索化。

1731337278343

为了区分lchild指针是指向左孩子还是前驱结点

定义以下规则：

  • ltag==0，指向左孩子；ltag==1，指向前驱结点
  • rtag==0，指向右孩子；rtag==1，指向后继结点

存储结构

17313191541681731319160066

左特征位 LTag= 0

lchild域指示结点的左孩子

lchild域指示结点的前驱结点

右特征位 RTag= 0

rchild域指示结点的右孩子

rchild域指示结点的后继结点

遍历

二叉线索树的遍历不需要递归，在先序/中序线索二叉树中，利用线索可一直向右遍历地找到当前结点的后继结点。因此，对有n个结点的二叉线索树，可以在 O(n) 时间内遍历完该树。

算法步骤

1731319477466

若二叉树p非空，

  1. 找到中序序列的第一个结点；
  2. 访问当前结点；
  3. 将当前结点的后继作为新的当前结点；
  4. 当前结点存在，则转2)

查找前驱/后驱结点

中序线索二叉树

  • p的后继

若p->RTag=1，则p->rchild即为所求；

若p->RTag=0，则从其右子沿着左链走到LTag=1

的那个结点就是。(右子树的最左的左孩子)

  • p的前驱

若p->LTag=1，则p->lchild即为所求；

若p->LTag=0，则从其左子沿着右链走到RTag=1

的那个结点就是。(左子树的最右的右孩子)

1731319530464

1
2
3
4
5
6
7
8
typedef  enum PointerTag {Link,Thread};
  // Link==0: 指针， Thread==1:线索
typedef struct BiThrNode {
    TElemType         data;
    Struct BiThrNode  *lchild, *rchild;
    PointerTag        LTag, RTag;
}BiThrNode, *BiThrTree;

中序线索化

  1. 每次处理完一个结点，我们将当前结点记作下一个结点的前驱结点
  2. 当前结点左结点为空时，令左结点指向前驱结点
  3. 当前驱结点右结点为空结点时，令前驱结点的右结点为当前结点
    上一个节点没有右结点时，将上一个结点接上当前节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
void inOrderThreadTree(Node* node)
{
	//如果当前结点为NULL 直接返回
	if (node == NULL) {
		return;
	}
	//先处理左子树
	inOrderThreadTree(node->left_node);
	if (node->left_node == NULL)
	{
		//设置前驱结点
		node->left_type = 1;
		node->left_node = pre;
	}
	//如果结点的右子节点为NULL 处理前驱的右指针
	if (pre !=NULL && pre->right_node == NULL)
	{
		//设置后继
		pre->right_node = node;
		pre->right_type = 1;
	}
	//每处理一个节点 当前结点是下一个节点的前驱
	pre = node;
	//最后处理右子树
	inOrderThreadTree(node->right_node);
}

遍历

由于在线索化的过程中每一个结点的右指针都非空（除最右叶结点），因此只需直接查找到最左结点再一直向右查找遍历即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void inOrderTraverse(Node* root)
{
	//从根节点开始先找到最左边
	if (root == NULL)
	{
		return;
	}
	Node* temp = root;
	//先找到最左边结点 然后根据线索化直接向右遍历
	while (temp != NULL && temp->left_type == 0)
	{
		temp = temp->left_node;
	}
	while (temp != NULL)
	{
		//输出
		temp = temp->right_node;
	}
}

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include<stdio.h>
#include<stdlib.h>
typedef struct Thread {
	struct Thread* left_node, *right_node;//左右指针
	int data;//需要存放的数据
	/*默认0代表左右孩子 1代表前驱或者后继*/
	int left_type;//类型标志
	int right_type;//类型标志
}Node;
 
Node* pre;//前驱结点的变量
Node* head;//头指针 指向某种遍历的第一个结点
 
void inOrderThreadTree(Node* node)
{
	//如果当前结点为NULL 直接返回
	if (node == NULL) {
		return;
	}
	//先处理左子树
	inOrderThreadTree(node->left_node);
	if (node->left_node == NULL)
	{
		//设置前驱结点
		node->left_type = 1;
		node->left_node = pre;
	}
	//如果结点的右子节点为NULL 处理前驱的右指针
	if (pre !=NULL && pre->right_node == NULL)
	{
		//设置后继
		pre->right_node = node;
		pre->right_type = 1;
	}
	//每处理一个节点 当前结点是下一个节点的前驱
	pre = node;
	//最后处理右子树
	inOrderThreadTree(node->right_node);
}
 
void inOrderTraverse(Node* root)
{
	//从根节点开始先找到最左边
	if (root == NULL)
	{
		return;
	}
	Node* temp = root;
	//先找到最左边结点 然后根据线索化直接向右遍历
	while (temp != NULL && temp->left_type == 0)
	{
		temp = temp->left_node;
	}
	while (temp != NULL)
	{
		//输出
		temp = temp->right_node;
	}
 
}

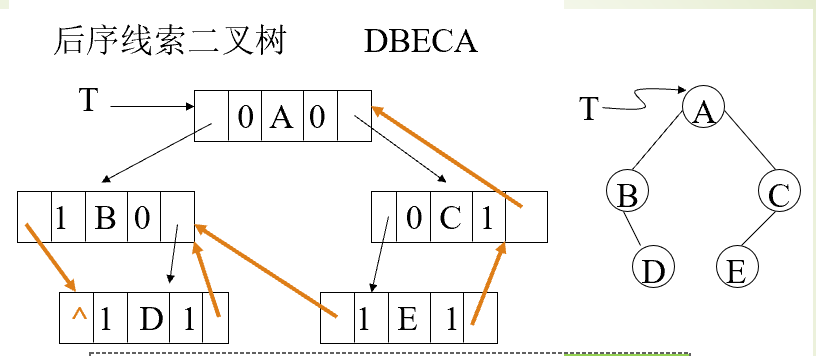
后序线索二叉树

后序和先序的线索二叉树的构建线索的逻辑与中序相似，只在对应的遍历顺序存在差异

  • p的前驱

若p->LTag=1，则p->lchild即为所求；

若p->LTag=0，

则若p->RTag=0， 则p->rchild即为所求

若p->RTag=1， 则p->lchild即为所求

  • p的后继

与双亲结点有关，因二叉链表中没有指向双亲结点的指针，就可能需通过二叉树的后序遍历才可确定，因而后序线索二叉树在此问题上并不比普通二叉树有效。

1731319863334

1
2
3
4
5
6
7
8
typedef  enum PointerTag {Link,Thread};
  // Link==0: 指针， Thread==1:线索
typedef struct BiThrNode {
    TElemType         data;
    Struct BiThrNode  *lchild, *rchild;
    PointerTag        LTag, RTag;
}BiThrNode, *BiThrTree;

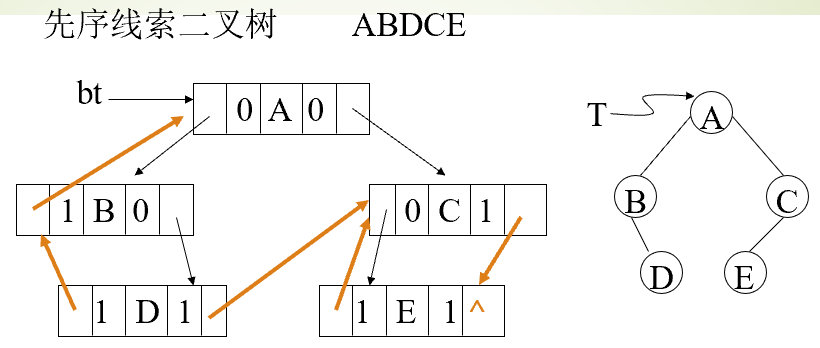
先序线索二叉树

与后序线索二叉树对偶

先序线索化

  1. 根节点：若左孩子为空，左孩子指向前驱结点，标记该前驱
  2. 若前驱结点不为空且其右孩子为空，则其右孩子指向当前节点
  3. 保存当前节点为前驱
  4. 先对当前节点进行线索化操作，再线索化左孩子、然后是右孩子

1731320007388

1
2
3
4
5
6
7
8
typedef  enum PointerTag {Link,Thread};
  // Link==0: 指针， Thread==1:线索
typedef struct BiThrNode {
    TElemType         data;
    Struct BiThrNode  *lchild, *rchild;
    PointerTag        LTag, RTag;
}BiThrNode, *BiThrTree;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
void inOrderThreadTree(Node* node)
{
	//如果当前结点为NULL 直接返回
	if (node == NULL) {
		return;
	}

	if (node->left_node == NULL)
	{
		//设置前驱结点
		node->left_type = 1;
		node->left_node = pre;
	}
	//如果结点的右子节点为NULL 处理前驱的右指针
	if (pre !=NULL && pre->right_node == NULL)
	{
		//设置后继
		pre->right_node = node;
		pre->right_type = 1;
	}
	//每处理一个节点 当前结点是下一个节点的前驱
	pre = node;
	//处理左子树
	inOrderThreadTree(node->left_node);
	//最后处理右子树
	inOrderThreadTree(node->right_node);
}

线索二叉树的更新操作

在线索二叉树上插入或删除一棵子树或者结点时，指针和线索都需作相应的改动。

[解决方法]

1）还原为普通二叉树，再重新将其线索化。

2）讨论可能出现的各种情况，寻找规律。

1731562466498

树和森林

树到二叉树的存储结构－－二叉链表表示法

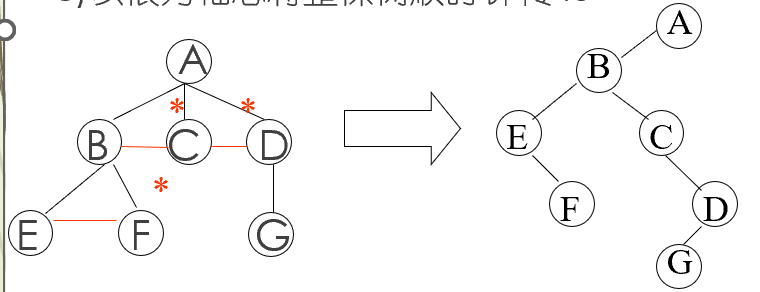
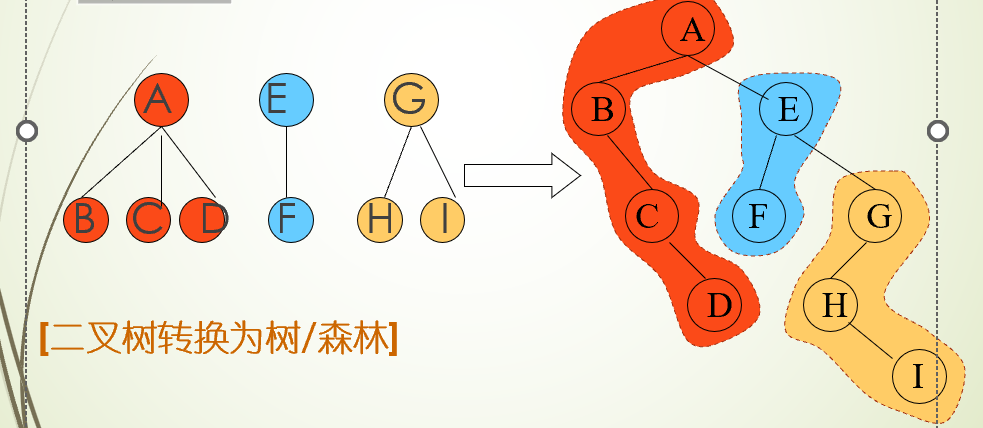
[树转换为二叉树]

1)在兄弟间加一连线

2)对每一结点，去掉它与孩子的连线(最左子除外)

3)以根为轴心将整棵树顺时针转45度

1731562578113

特点：根无右子树，左支是孩子，右支是兄弟

[森林转换为二叉树]

1)先将森林里的每一棵树转换成一棵二叉树

2)从最后一棵树开始，把后一棵树的作为前一棵树的根的右子

1731562721387

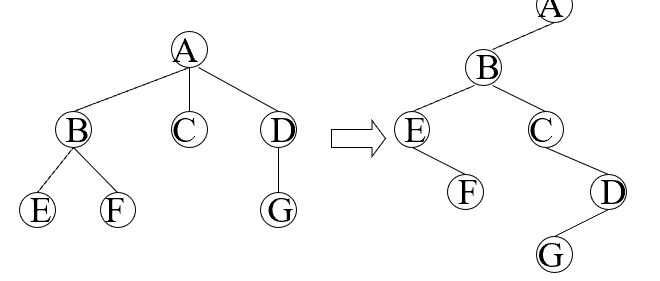
树的遍历（先转成二叉树再遍历）

先(根)序遍历 先访问树的根结点，然后依次先根遍历根的每棵子树 ABEFCDG(二叉树先序)

后(根)序遍历 先依次后根遍历根的每棵子树，然后访问树的根结点 EFBCGDA(二叉树中序)

层次遍历 若树不空，则自上而下自左至右访问树中每个结点 ABCDEFG1731562791643

森林的遍历

1731562904454

树的存储结构

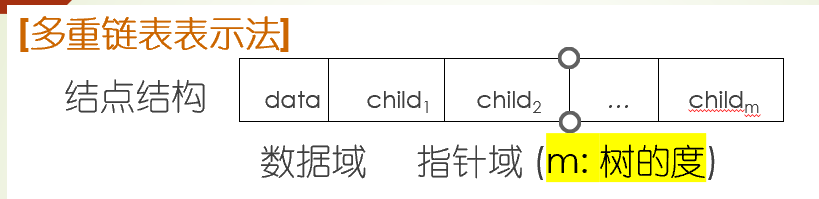
1731562966438

1
2
3
4
5
6
#define   TREE_DEGREE    100
typedef struct MultiTNode {
  TElemType  data;
  struct MultiTNode * ptr[TREE_DEGREE]
}MultiTNode, * MultiTree;

  • Title: 哈夫曼树
  • Author: time will tell
  • Created at : 2024-11-16 10:48:33
  • Updated at : 2024-11-16 17:34:42
  • Link: https://sbwrn.github.io/2024/11/16/哈夫曼树/
  • License: This work is licensed under CC BY-NC-SA 4.0.
Comments
On this page
哈夫曼树
  1. 1. 赫夫曼树（最优二叉树）
    1. 1.1. 引入
    2. 1.2. 赫夫曼算法：构造最优二叉树
      1. 1.2.0.1. [基本思想]使权大的结点靠近根
      2. 1.2.0.2. [算法思路]
      3. 1.2.0.3. [操作要点]对权值的合并、删除与替换，总是合并当前值最小的两个
  2. 1.3. 赫夫曼树的存储结构
    1. 1.3.1. 顺序存储
    2. 1.3.2. 构造算法
  3. 1.4. 赫夫曼编码
    1. 1.4.1. 前缀编码
      1. 1.4.1.0.1. 特点：
      2. 1.4.1.0.2. 译码过程：
  4. 1.4.2. 赫夫曼编码码表构造
  • 2. 线索二叉树
    1. 2.1. 线索化
    2. 2.2. 存储结构
    3. 2.3. 遍历
      1. 2.3.1. 算法步骤
      2. 2.3.2. 查找前驱/后驱结点
        1. 2.3.2.1. 中序线索二叉树
        2. 2.3.2.2. 中序线索化
        3. 2.3.2.3. 遍历
        4. 2.3.2.4. 完整代码
      3. 2.3.3. 后序线索二叉树
      4. 2.3.4. 先序线索二叉树
        1. 2.3.4.1. 先序线索化
    4. 2.4. 线索二叉树的更新操作
      1. 2.4.0.1. [解决方法]
  • 2.5. 树和森林
    1. 2.5.1. 树到二叉树的存储结构－－二叉链表表示法
      1. 2.5.1.1. [树转换为二叉树]
      2. 2.5.1.2. [森林转换为二叉树]
      3. 2.5.1.3. 树的遍历（先转成二叉树再遍历）
      4. 2.5.1.4. 森林的遍历
    2. 2.5.2. 树的存储结构