数组与广义表

本章所介绍的数组既可以是顺序的,也可以是链式结构
数组和线性表的关系以及数组的运算
任何数组A都可以看作一个线性表
A=(a1,a2, …, ai , …an)
表中每一个元素ai是一个(n-1)维数组
数组是线性表的拓展,其数据元素本身也是线性表
数组的特点
–数组中各元素都具有统一的类型
–可以认为,d维数组的非边界元素具有d个直接前趋和d个直接后继
•以二维数组为例:上和左,下和右;多维以此类推
–数组维数确定后,数据元素个数和元素之间的关系不再发生改变,适合于顺序存储
•什么情况下考虑链式存储或其他存储?
–每组有定义的下标都存在一个与其相对应的值
因此:
–给定一组下标,取得相应的数据元素值, Value
–给定一组下标,修改相应的数据元素值, Assign
数组的顺序存储结构
一维数组:ElemType a[n];
1 | 方法一:LOC[i]=LOC[0]+iL |
二维数组:ElemType a[m][n];
“行序为主序” 即 “低下标优先”
“列序为主序” 即 “高下标优先”
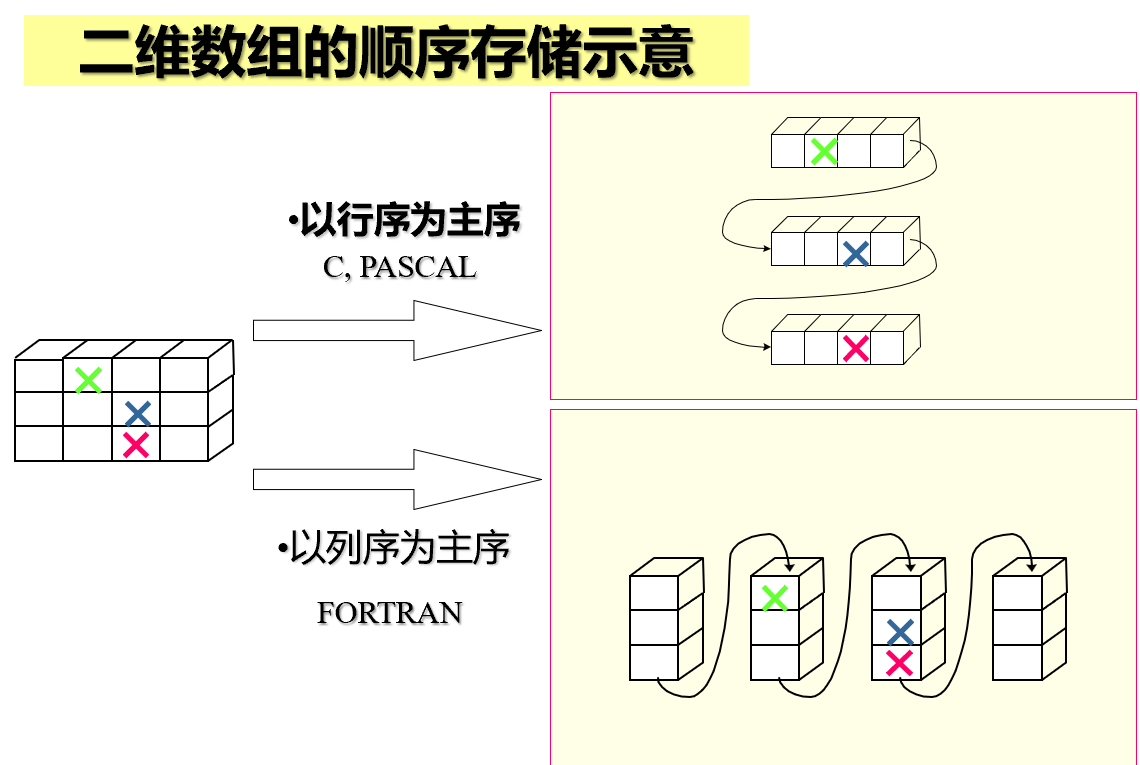
二维数组a[m][n],各维元素个数为m,n。设数组开始存放位置 LOC(0, 0 ) = b,行序优先方式的顺序存储时,a[i][j]存放位置:
方法一:LOC ( i, j ) = b + (i*n+j)*L
方法二:
1 | LOC[i,j] = LOC[0,0]+(in+j)L = c0 + c1xi + c2xj |
n维数组:ElemType a[m1][m2] … [mn] ;
各维元素维度分别 m1, m2, m3, …, mn,按维度先后次序进行顺序存储。上述a数组按顺序存储m1 个n-1维的数组,其中每个n-1维数组又是按顺序存储了m2个n-2维的数组,以此类推。
这样下标为i1, i2, i3 … in 的n维数组元素的存储位置:
1 | 方法一:𝐿𝑂𝐶(𝑖_1,𝑖_2,…𝑖_𝑛 )=𝑎+〖( 𝑖〗_1∗𝑚_2∗𝑚_3∗…∗𝑚_𝑛 |
1 | 通式(方法二): |
矩阵的压缩存储(压缩从而节省空间)
带状矩阵
在n´n的方阵中,非零元素集中在主对角线及其两侧共L(奇数)条对角线的带状区域内L对角矩阵
因此只需要存储带状区内的元素

除首行和末行,按每行L个元素,共(n-2)L+(L+1)=(n-1)L+1 个元素。
1 | 存储地址计算: k=(i-1)L+(j-i) |
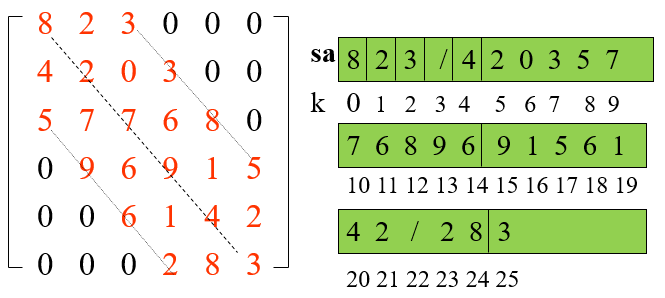
随机稀疏矩阵
[特点] 大多数元素为零。
[常用存储方法] 记录每一非零元素(i,j,aij )
—节省空间,但丧失随机存取功能
•顺序存储:三元组表
•链式存储:十字(正交)链表
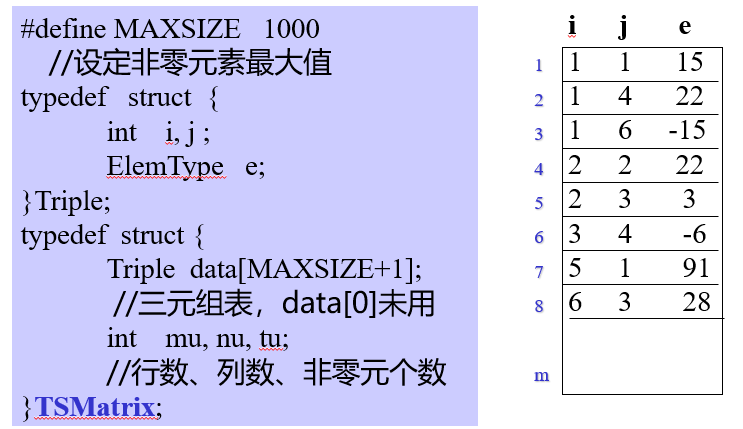
三元组表
用行数、列数和存储的值来表示数据在随机稀疏矩阵中的元素
求三元组表的转置矩阵
普通算法:
1 | void TransMatrix(TSMatrix &b, TSMatrix a) |
将每个坐标的i、j值交换
但是注意,因为是顺序排列,所以对原组表遍历时需要从每一列来寻找
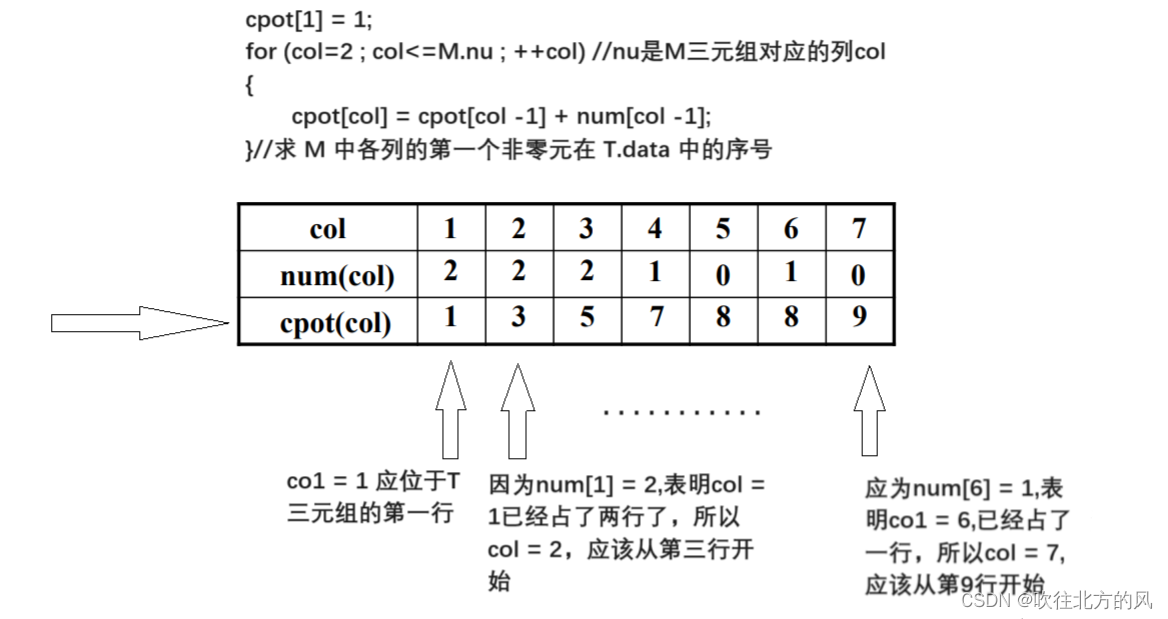
快速转置法:
引入两个辅助向量:
–num[1: a.nu]:a中每列的非零元素个数
–cpot[1: a.nu]:a中每列的第一个非零元素在b中的位置
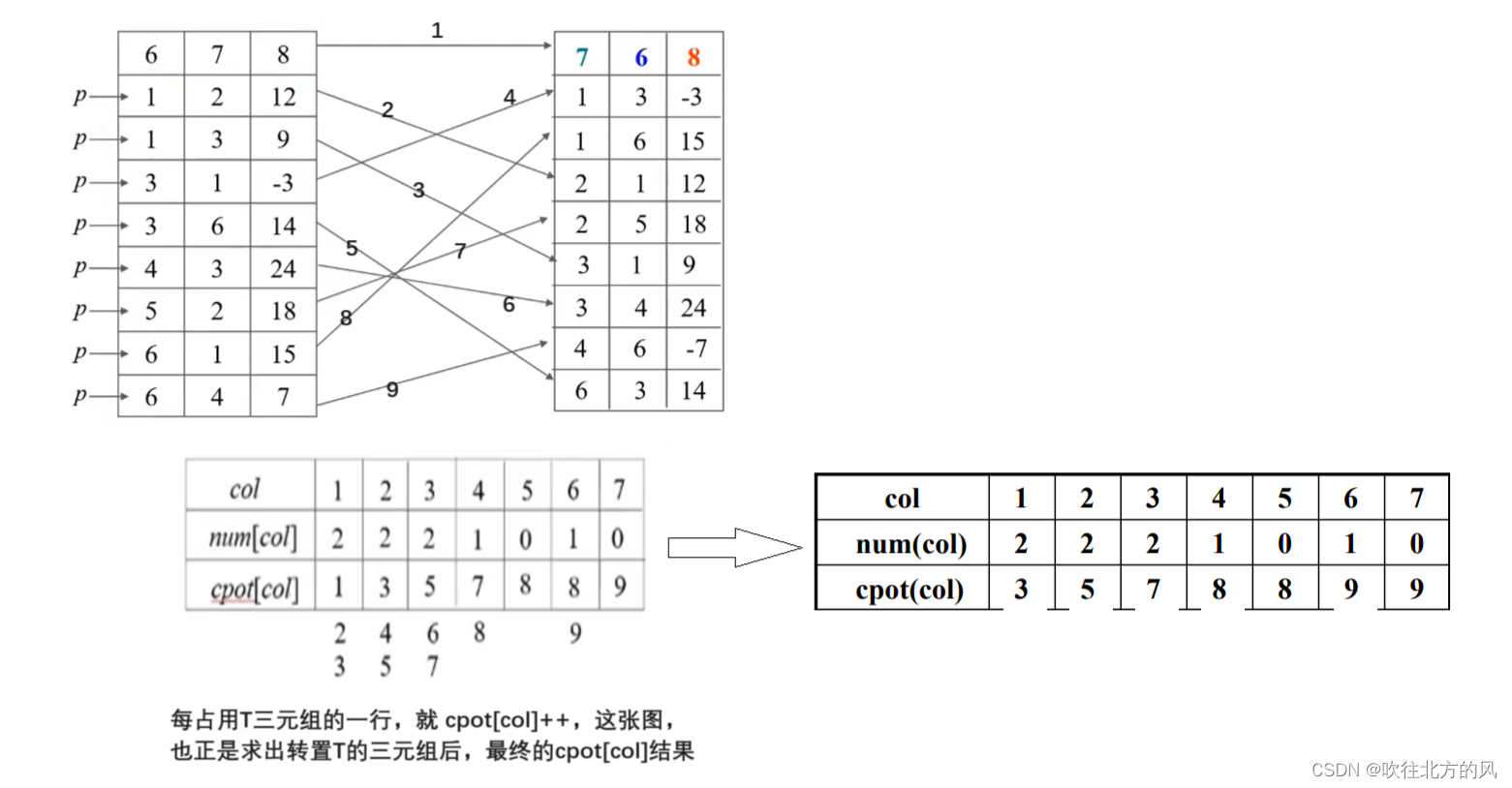
1 | Statue FastTransMatrix(TSMatrix &b, TSMatrix a) |
行逻辑连接的表
便于随机存取任意一行的非零元素。
数组的行是连续存储的。这种存储方式在内存中按行优先顺序存储数组元素。每个元素的内存地址可以通过 i * cols + j 计算,其中 i 是行索引,j 是列索引,cols 是列数。
1 |
|
这种存储方式在处理多维数组时非常高效,特别是在需要按行访问数组元素的情况下。因此在稀疏矩阵相乘时比较简便。
十字(正交)链表
在行、列两个方向上,将非零元素链接在一起。克服三元组表在矩阵的非零元素位置或个数经常变动时的使用不便。
每个结点包含四个指针,分别指向同一行的下一个结点、同一列的下一个结点、同一行的前一个结点和同一列的前一个结点。
1 | typedef struct OLNode |
广义表
广义表本质上是非线性结构,是扩展的线性表:表中的数据元素本身也是一个数据结构。
定义
广义表是由零个或多个原子或者子表组成的有限序列。可以记作:LS=(d1, d2, … , dn)
**原子:逻辑上不能再分解的元素。**
**子表:作为广义表中元素的广义表。**
广义表中的元素全部为原子时即为线性表。线性表是广义表的特例,广义表是线性表的推广。
表示
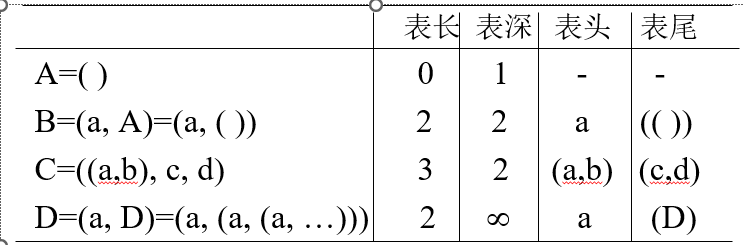
表的长度 : 表中的元素(第一层)个数。
表的深度 : 表中元素的最深嵌套层数。
表头: 表中的第一个元素。
表尾: 除第一个元素外,剩余元素构成的广义表。
非空广义表的表尾必定仍为广义表。
因此可以直接通过取表头、取表尾对广义表进行操作
图形仅供参考
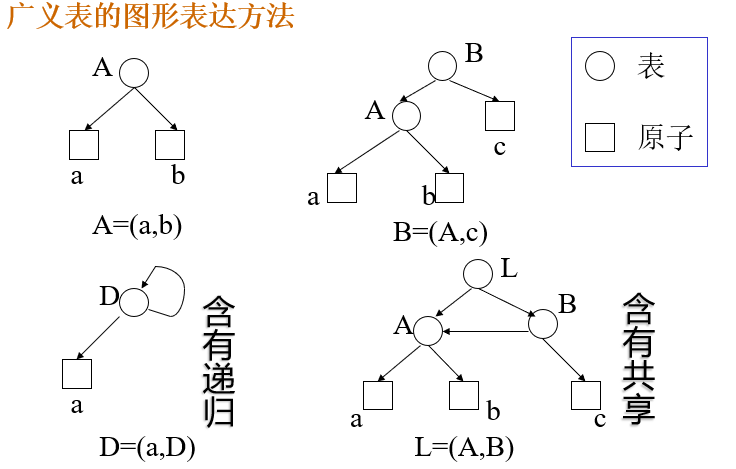
广义表的长度和深度
此处重点强调一下广义表的长度和深度
广义表的长度,指的是广义表中所包含的数据元素的个数。
在计算元素个数时,广义表中存储的 每个原子算作一个数据,同样 每个子表也只算作是一个数据。
- LS = {a1,a2,…,an} 的长度为 n;
- 广义表 {a,{b,c,d}} 的长度为 2;
- 广义表 { {a,b,c} } 的长度为 1;
- 空表 {} 的长度为 0。
- 其实就是第一层元素和子表个数的和
广义表的深度,可以通过观察该表中所包含括号的层数间接得到
广义表结构的分类
•纯表:与树型结构对应的广义表。
•再入表:允许结点共享的广义表。
•递归表:允许递归的广义表。
递归表>再入表>纯表>线性表
广义表的复制
任意一个非空广义表来说,都是由两部分组成:表头和表尾。反之,只要确定的一个广义表的表头和表尾,那么这个广义表就可以唯一确定下来。
对于表头可能是
- 子广义表
- 单原子
对于表尾则一定是广义表:
- 非空广义表
- 空广义表
所以停止递归的条件有两个:
- 表头是一个单原子
- 表头/表尾是一个空表
因此复制一个广义表,也是不断的复制表头和表尾的过程。如果表头或者表尾同样是一个广义表,依旧复制其表头和表尾。
抽象数据类型定义

广义表的存储结构
方法1—头尾链表形式
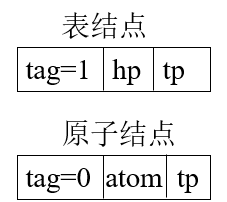
1 | typedef enum {ATOM, LIST} ElemTag; |
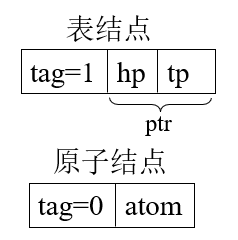 hp:表头的指针、tp:表尾的指针
hp:表头的指针、tp:表尾的指针
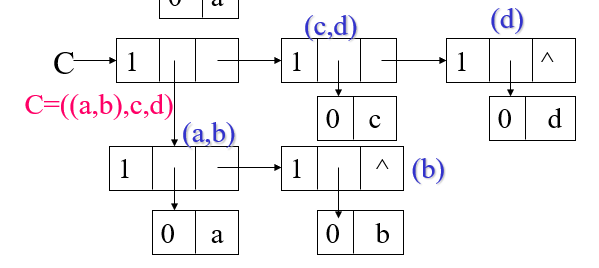
方法2—扩展的线性链表形式
1 | typedef enum {ATOM, LIST} ElemTag; |
 hp: 指向表头的指针、tp: 指向同一层的下一个结点;构成一个单链表,把本层的原子或主表都链起来了。
hp: 指向表头的指针、tp: 指向同一层的下一个结点;构成一个单链表,把本层的原子或主表都链起来了。
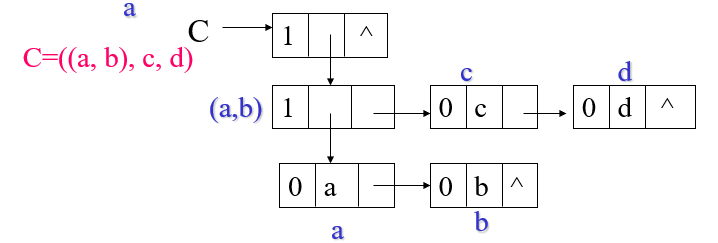
广义表的递归算法
广义表的特点:定义是递归的。
示例约定:非递归表且无共享子表。
[示例1]计算广义表的深度

1 | int GListDepth(GList1 L) |
[示例2]
复制广义表
复制广义表的过程,其实就是 不断的递归复制广义表中表头和表尾的过程,递归的出口有两个:
- 如果当前遍历的数据元素为空表,则直接返回空表。
- 如果当前遍历的数据元素为该表的一个原子,那么直接复制,返回即可
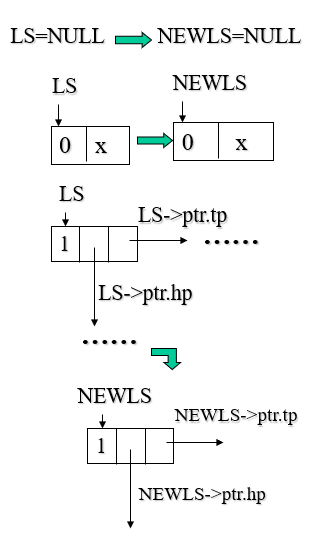
1 | // 广义表的复制, C为复制目标广义表,*T为指向复制后的广义表 |
- Title: 数组与广义表
- Author: time will tell
- Created at : 2024-11-16 10:49:25
- Updated at : 2024-11-28 13:14:44
- Link: https://sbwrn.github.io/2024/11/16/数组与广义表/
- License: This work is licensed under CC BY-NC-SA 4.0.
