串 | 日薄西山

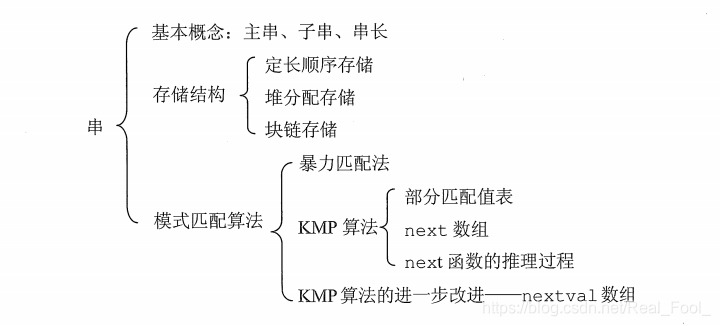
一、串的定义

串( string)是由零个或多个字符组成的有限序列，又名叫字符串。

一般记为：S = ′ a 1 a 2 . . . a n ′ ( n > = 0 )

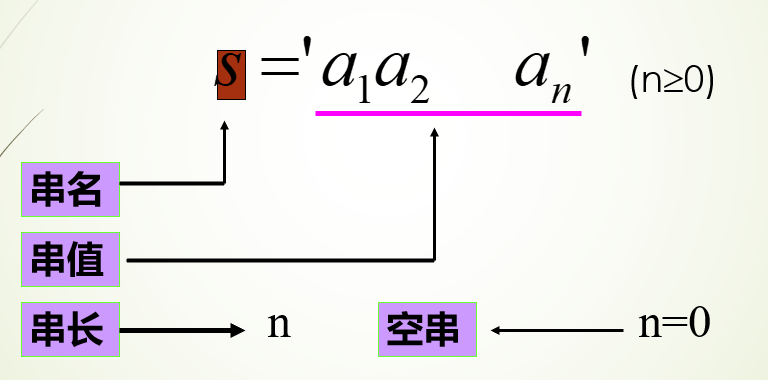
另外还有一些其它概念：

空串：空串不包含任何字符，表示为，长度为0。
空格串：是只包含空格的串。注意它与空串的区别，空格串是有内容有长度的，而且可以不止一个空格。
子串与主串：串中任意个数的连续字符组成的子序列称为该串的子串，相应地，包含子串的串称为主串。
子串在主串中的位置就是子串的第一个字符在主串中的序号。

逻辑结构上，串与线性表极为相似，区别仅在于串的数据对象限定为字符集。

而基本操作上，串和线性表有很大差别。线性表的基本操作主要以单个元素作为操作对象，如查找、插入或删除某个元素等;而串的基本操作通常以子串作为操作对象，如查找、插入或删除一个子串等。

二、串的存储结构

1、定长顺序存储表示

类似于线性表的顺序存储结构，用一组地址连续的存储单元存储串值的字符序列。在串的定长顺序存储结构中，为每个串变量分配一个固定长度的存储区，即定长数组。

#define MAXLEN 255	//预定义最大串长为255
typedef struct{
	char ch[MAXLEN];	//每个分量存储一个字符
	int length;	//串的实际长度
}SString;

在定长顺序存储中，串的实际长度只能小于等于MAXLEN，超过预定义长度的串值会被舍去，称为截断。

同时串长有两种表示方法: 一是用一个额外的变量len来存放串的长度;二是在串值后面加一一个不计入串长的结束标记字符“\0”，此时的串长为隐含值，可用strlen提取

2、堆分配存储表示

堆分配存储表示仍然以一组地址连续的存储单元存放串值的字符序列，但它们的存储空间是在程序执行过程中动态分配得到的。

typedef struct{
	char *ch;	//按串长分配存储区，ch指向串的基地址
	int length;	//串的长度
}HString;

如果使用两者直接的空间分配，则无截断一说

Status Concat(HString &T,  HString  S1, HString S2)
//返回串S1和S2联接而成的新串T，没有截断一说了
{   
    if(T.ch)   free(T.ch);   //释放T原有空间
    if(!(T.ch=(char *)malloc((S1.length+S2.length)*sizeof(char))))
        return OVERFLOW;
    T.length=S1.length+S2.length;
    T.ch[0..s1.length-1]=S1.ch[0..s1.length-1];
    T.ch[S1.length.. T.length-1]=S2.ch[0..S2.length-1];
    return OK;
} // Concat

3、块链存储表示

类似于线性表的链式存储结构，也可采用链表方式存储串值。由于串的特殊性(每个元素只有一个字符)，在具体实现时，每个结点既可以存放一个字符，也可以存放多个字符。每个结点称为块，整个链表称为块链结构。图(a)是结点大小为4 (即每个结点存放4个字符)的链表,最后一个结点占不满时通常用“#”补上;图(b)是结点大小为1的链表。

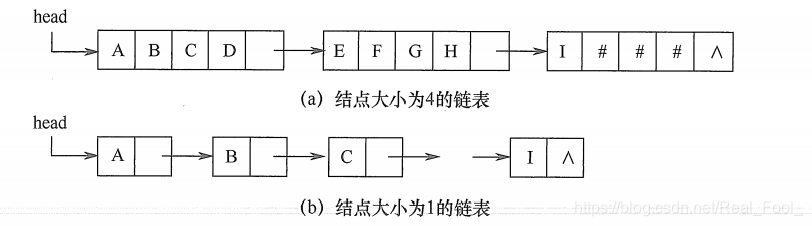
结构定义如下：

#define CHUNKSIZE  4           //由用户定义块大小
typedef  struct  Chunk  {
         char  ch[CHUNKSIZE];
         struct Chunk * next;
}Chunk;
typedef  struct  {   //头尾指针的单链表，结点的data是字符块
    Chunk * head， * tail;    //串的、尾头指针
    int    curlen;           //串的当前长度
}LString;

但是由于占用存储量大且操作不便，实际应用很少

三、串的基本操作

仅供了解即可，需要可尝试自己实现

StrAssign(&T, chars): 赋值操作。把串T赋值为 chars
Strcopy(&T, S): 复制操作。由串S复制得到串T。
StrEmpty(S): 判空操作。若S为空串,则返回TRUE,否则返回 FALSE
StrCompare(S,T): 比较操作。若S>T,则返回值>0;若S=T,则返回值=0;若S<T,则返回值<0。
StrEngth(S): 求串长。返回串S的元素个数
Substring(&Sub,S,pos,1en):求子串。用Sub返回串S的第pos个字符起长度为len的子串。
Concat(&T,S1,S2): 串联接。用T返回由S1和S2联接而成的新串。
Index(S,T): 定位操作。若主串S中存在与串T值相同的子串,则返回它在主串S中第一次出现的位置;否则函数值为0
Clearstring(&S): 清空操作。将S清为空串
Destroystring(&S): 销毁串。将串S销毁
不同的高级语言对串的基本操作集可以有不同的定义方法。在上述定义的操作中,串赋值StrAssign、串比较 StrCompare、求串长 Strength、串联接 Concat及求子串 Substring五种操作构成串类型的最小操作子集,即这些操作不可能利用其他串操作来实现;反之,其他串操作(除串清除 Clearstring和串销毁 Destroystring外)均可在该最小操作子集上实现。

例如,可利用判等、求串长和求子串等操作实现定位函数 Index(S,T)。

int Index(Sring S, String T){
	int i = 1, n = StrLength(S), m = StrLength(T);
	String sub;
	while(i <= n-m+1){
		SubString(sub, S, i, m);	//取主串第i个位置，长度为m的串给sub
		if(StrCompare(sub, T) != 0){
			++i;
		}else{
			return i;	//返回子串在主串中的位置
		}
	}
	return 0;	//S中不存在与T相等的子串
}

四、串的模式匹配（重点）

1、简单的模式匹配算法

子串的定位操作通常称为串的模式匹配，它求的是子串(常称模式串)在主串中的位置。这里采用定长顺序存储结构，给出一种不依赖于其他串操作的暴力匹配算法。

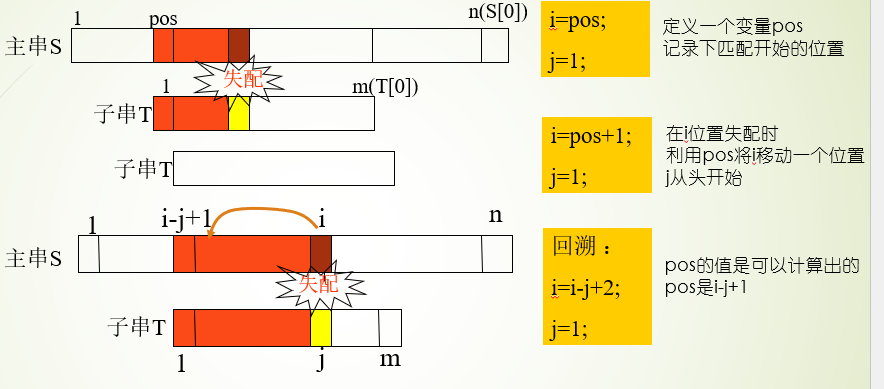
BF算法基本思想

将主串的第pos个字符(用i跟踪)和模式的第一个字符(用j跟踪)比较，

若相等，继续逐个比较后续字符(i++;j++)；

若不等，从主串的下一字符起(i=i-j+2)，重新与模式的第一个字符(j=1)比较。

int  Index(SString S, SString T, int pos)
{
    int j=1, i=pos;   
    while( i <= S[0]  && j <= T[0])
    {
        if( S[ i ]==T[ j ]) {++i;  ++j; }
        else { i=i-j+2; j=1;} //i回溯，j回到1
	  }
    if( j > T[0] ) 
        return i - T[0];
    else 
        return 0;
}

**总次数为：(n-m)m+m＝(n-m+1)m

若m<<n，则算法复杂度O(n*m)

2、KMP算法

利用已经部分匹配的结果而加快模式串的滑动速度

我们引入一个next数组，将j后退时对应的k的值保存在next[j]：

next[ j ]的含义是:在子串的第j个字符与主串发生失配时,则跳到子串的next[ j ]位置重新与主串当前位置进行比较。

在S[i] 和T[j]失配时(S[i] != T[j])，可继续对S[i] 和 T[next[j]]
进行比较。

此时，S串的 i不需要回溯到 i-j+2的位置重新开始，而是停在原地不动；

当存在k时，T串的j只需要回溯到next[j]的位置；不存k时回溯到1。

int Index_1(SString S, SString T,
            int pos)
{
  int j=1, i=pos;   
  while(i<=S[0] && j<= T[0])
  {
    if( S[i]==T[j])
    {++i;  ++j; }
    else
    {
       if(j==1) i++;
       else j=next[j];
    }
  }
  if( j > T[0] ) 
    return i - T[0];
  else 
    return 0;
}

next[j]表示的是j回退到位置，j==1时已经没有回退的位置了，所以只能给个0

那么规定，next[1]=0，以便使用next[1]：

int Index_KMP(SString S, SString T,
            int pos)
{
  int j=1, i=pos;   
  while(i<=S[0] && j<= T[0])
  {
    if( S[i]==T[j])
    {++i;  ++j; }
    else
    {
       j = next[j];//当j为1时，将被赋值为0
       //此时j==0了，可以和i一起++了  
    }
  }
  if( j > T[0] ) 
    return i - T[0];
  else 
    return 0;
}

那么接下来的问题是如何计算出next[j]，使得可以直接依据当前匹配情况缩减匹配次数

计算next[i]算法思路

经过分析，除第一个字符外，模式串中其余的字符对应的next数组的值等于其最大公共前后缀长度加上1

理论上是这样的

但是我看不懂

求next数组的程序如下：(注：这里的字符串以下标1为起点，如以下标0为起点请找到F盘中1027中修改的代码，并更改Index函数的判断条件)

void get_next(String T, int *next){
	int i = 1, j = 0;
	next[1] = 0;
	while (i < T.length){
		if(j==0 || T.ch[i]==T.ch[j]){	//ch[i]表示后缀的单个字符，ch[j]表示前缀的单个字符
			++i; ++j;
			next[i] = j;	//若pi = pj， 则next[j+1] = next[j] + 1
		}else{
			j = next[j];	//否则令j = next[j]，j值回溯，循环继续
		}
	}
}

next函数的改进：将在KMP中的T向前比较改为在生成next值时进行，由于生成时从前向后生成，在生成i位置的next值时，只需向前比较一次即可。

void get_nextval(SString T, int nextval[])
{
    i= 1; nextval[1] = 0; j = 0;   
    while( i<T[0]){
        if(j==0 || T[i] == T[j]){
            ++i; ++j; 
            if(T[i] != T[j]) nextval[i] = j;
            else  nextval[i] = nextval[j];
         }
         else  
             j = nextval[j];
     }
}                       

两次生成的next数组应该大部分情况都不太一样，但是效应应该没有区别。