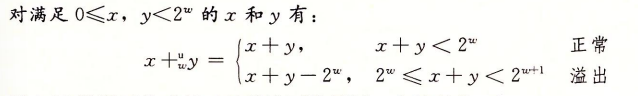2.1.2 字数据大小

字长：辨明指针数据的标称大小

64位机可以运行32位机器的程序：向后兼容

2.1.3 寻址和字节顺序

小端法：最低有效位在最前面的方式

小端法机器生成的机器级程序表示时，最低位字节在左边，最高字节在右边，刚好与正常书写的方式相反

大端法：最高有效字节在最前面的方式

反汇编器：确定可执行程序文件所表示的指令序列的工具

2.1.8 c语言中的逻辑运算

||、&&、!

2.1.9 c语言中的移位运算

算术左移、右移：<< 、>>

负数算术右移时会在高位补1

逻辑左移、右移：<<<、>>>

负数逻辑右移时会在高位补0

2.2.2 无符号数的编码

1. 无符号数的表示

无符号数的编码是指使用固定位数（二进制位）来表示非负整数的一种方法。与有符号数不同，无符号数没有负号或正号的位，所有位都用来表示数值本身。因此，它只能表示正整数和零。

另外，在c语言中引用头文件 #include<limits.h>可以调用一些系统中规定的上下限值

无符号数的表示

无符号数用 (w) 位二进制表示时，可以表示的数值范围为：

其中，(w) 表示位数。

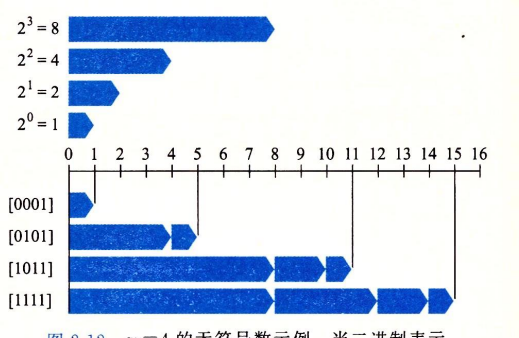
其形象如下

最多可以表示 2w 个比特位 ：无符号数可以使用全部的 w 位来表示数值，没有符号位，因此其取值范围是从 0 到最大值

例如：

4 位无符号数能表示的数值范围为 (0) 到 (2^4 - 1 = 15)，即 [0, 15]。4 位无符号数的编码如下：
- 0000 表示 0
- 0001 表示 1
- 0010 表示 2
- 0111 表示 7
- 1111 表示 15

2. 无符号数的编码规则

无符号数的编码就是简单的二进制数表示法，从零开始，逐次递增：

最低位表示 (2^0 = 1)
第二位表示 (2^1 = 2)
第三位表示 (2^2 = 4)
依此类推，最高位表示 (2^{w-1})

每一位上的数值要么是 0，要么是 1，通过这些位的组合来表示不同的数值。例如，对于 8 位无符号数，编码方式如下：

00000000 表示 0
00000001 表示 1
00000010 表示 2
…
11111111 表示 255

3.无符号数的加法

无符号加法类似于普通加法，但需要关注进位的处理。在计算时，每一位相加如果超过二进制系统的表示范围（通常是 0 或 1），则产生进位。
如果加法结果超出所能表示的位数范围（比如 8 位无符号数最大可以表示 255，超过 255 会发生溢出），那么会出现溢出现象。溢出会使结果在二进制中重新从0开始计数。
例：
1
2
3
4
5
240 (1111 0000)
+ 30 (0001 1110)
--------------
270 结果（因为超过255，因此发生溢出，实际存储结果为 14（0000 1110））
即

4.无符号数的减法

无符号减法则类似于普通减法，但要处理借位问题。借位与加法中的进位相似，当某个位数不够减时，需要从高位借位。
如果结果为负数（即减数大于被减数），在无符号数中会表现为一个非常大的正数，因为计算机会假设没有负数的概念，从而发生下溢。

  30 (0001 1110)
- 240 (1111 0000)
--------------
  -210   结果在无符号数中无法表示，实际存储为 46（0010 1110））

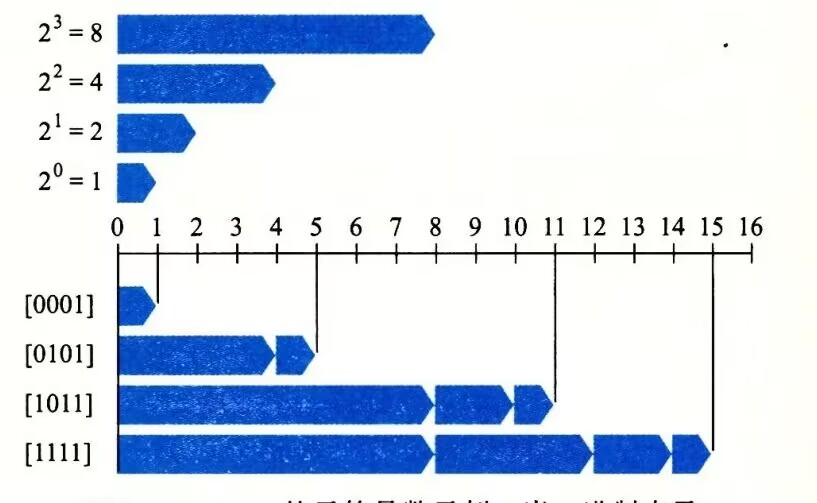
5.无符号数乘法的基本规则

无符号数乘法遵循以下规律：

乘法若大于w位则会被截断

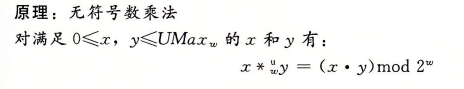
同时在计算溢出位时，可以注意到

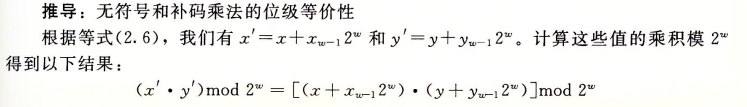
乘法示例

假设我们进行两个 4 位无符号数的乘法计算：

a=10102a = 1010_2a=10102 （即 10）
b=01102b = 0110_2b=01102 （即 6）

那么我们将这两个数相乘：

  1010    (a = 10)
× 0110    (b = 6)
--------
  0000    (a × 0)
 10100    (a × 1，向左移一位)
 101000   (a × 1，向左移两位)
--------
 111100   (a × b = 60)

6.无符号数位操作

按位取反：~x=-x-1

7、无符号数的取反

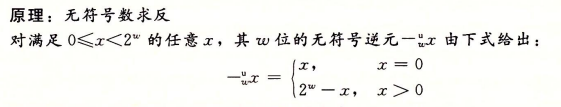
补码与无符号数之间的联系

通过无符号数和补码各自的成分图可以推断

二进制转反码：除了最高有效位的权是-(2^(w-1)-1)而不是-2^(w-1)，其与补码一致

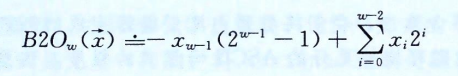
二进制转原码：最高有效位是符号位，用来确定剩下的位应该取负权还是正权

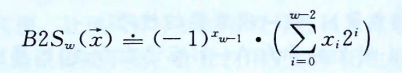
2.2.4 有符号数和无符号数之间的转换

补码和无符号数之间存在直接的转换方式

当将一个有符号数映射为它相应的无符号数时，负数转换成了大的正数，非负数保持不变

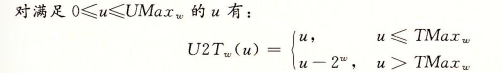
直观表示如下图所示

2.2.5 C语言中的有符号数与无符号数

C语言中几乎所有情况下都使用补码，大多数数字都默认有符号

在printf输出的过程中，printf没有使用任何类型信息，意味着其可以用指示符%u来输出int类型的数值，也可以使用%d来输出unsigned类型的数值

当执行一个运算时，如果它的一个运算数是有符号的而另一个是无符号的，那么C语言会隐式地将有符号参数强制类型转换为无符号数，并假设这两个数都是非负的，来执
行这个运算。就像我们将要看到的，这种方法对于标准的算术运算来说并无多大差异，但
是对于像<和>这样的关系运算符来说，它会导致非直观的结果。

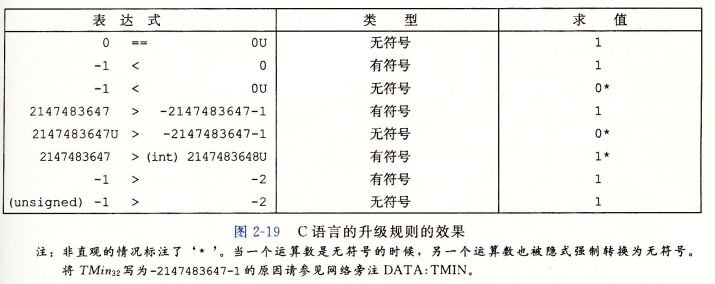
2.2.6 扩展数字位表示

2.3 整数运算

根据无符号数四则运算的补码运算

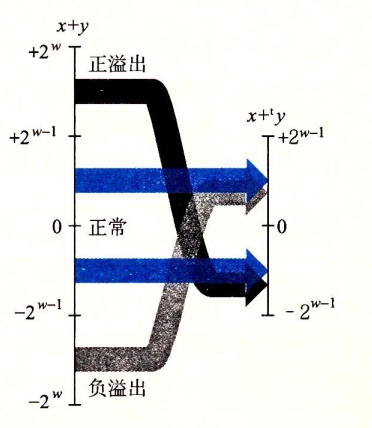
1.补码加法

对于溢出情况，补码会从临界反向往中心靠拢

2.补码的非

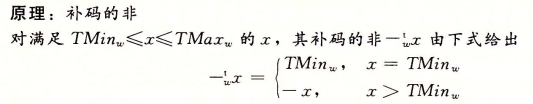
对w位的补码加法来说，TMinw是自己加法的逆，而对其他任何数值x都有-x作为其加法的逆

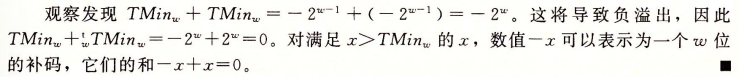
3.补码乘法

与无符号数一样，补码在遇到溢出时，也会对位级进行截断

在移位的同时加/减自身

4.补码除法

整数除法总是舍人到零（记住！！是向零取整的）。为了准确进行定义，我们要引入一些符号。对于任何实数a，定义[a」为唯一的整数a’，使得 a’≤a<a’+1。例如，[3.14」=3,[-3.14」=-4而[3]=3。同样，定义「a]为唯一的整数 a’，使得 a’-1<a≤a’。例如,[3.14]=4,[-3.14]=-3而[3]=3。对于x>0和y>0，结果会是[x/y」，而对于x<0和y>0，结果会是[x/y]
也就是说，它将向下舍人一个正值，而向上舍人一个负值。

因此，在计算负数的除法时，会遇到向下取舍的情况

这时就需要引入偏移量的概念，由于偏移量只影响被移除的位，在执行算术右移之前加上一个适当的偏置量是才能导致结果正确舍入，下图的示例演示了偏移量的作用

偏移量：（1<<k)-1

2.4 浮点数

2.4.1 二进制小数

二进制简单定义：

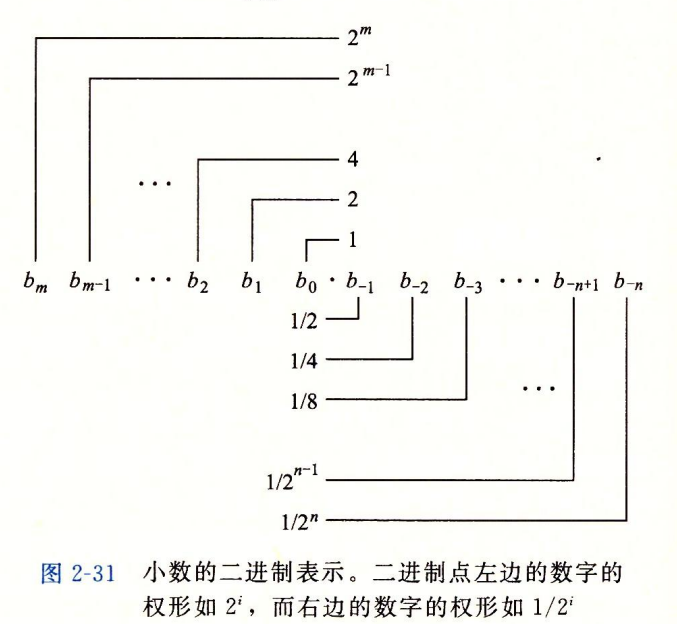
但是考虑有限长度的编码，二进制并不能准确地表示一个十进制小数

2.4.2 IEEE浮点表示

定点表示法不能很有效地表示非常大的数字，例如5 * 2^100实际上使用了101后面跟随100个零的位模式来表示。相反，我们希望通过给定x和y的值，来表示形如x * 2^y的数

第二章 信息的表示和处理