栈和队列 | 日薄西山

定义和特点

栈和队列是两种基本的数据结构，它们的特点是先进后出和先进先出。

栈的定义和特点

栈:受约束的线性表，只允许栈顶元素入栈和出栈
对栈来说，表尾端称为栈顶，表头端称为栈底，不含元素的空表称为空栈
先进后出，后进先出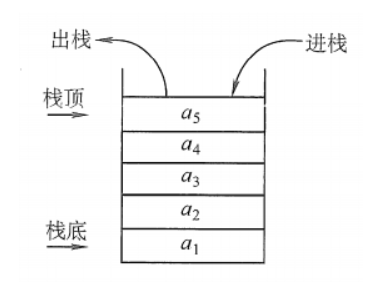

队列的定义和特点

队列:受约束的线性表，只允许在队尾插入，在队头删除
先进先出，后进后出

栈的表示和操作实现

顺序栈的表示：存储结构

-----顺序栈的存储结构-----
#define MAXSIZE 100         //顺序栈存储空间的初始分配址
typedef struct{
    SElemType *base;        //栈底指针
    SElemType *top;         //栈顶指针
    int stacksize;          //栈可用的最大容扯
  
}Sqstack;

数组实现简略版

#define MAXSIZE 50  //定义栈中元素的最大个数
typedef int ElemType;   //ElemType的类型根据实际情况而定，这里假定为int
typedef struct{
    ElemType data[MAXSIZE];
    int top;    //用于栈顶指针
}SqStack;

top 指栈顶元素后一位置

S.top == 0时，栈空
S.top == stacksize 时，栈满

顺序栈操作的实现:初始化

Status InitStack(SqStack&S){
    //构造一个空栈S
    S.base=(SElemType *)mallo(STACK_INIT_SIE* sizeof(SElemType));   
    if(!S.base)exit(OVERFLOW);  //存储分配失败
    S.top = S.base;
    S.stacksize = STACK_INIT_SIZE:
    return OK;
}//Initstack

顺序栈操作的实现:入栈

/*插入元素e为新的栈顶元素*/
Status Push(SqStack *S, ElemType e){
    //满栈
    if(S->top == MAXSIZE-1){
        return ERROR;
    }
    S->top++;   //栈顶指针增加一
    S->data[S->top] = e;    //将新插入元素赋值给栈顶空间
    return OK;
}

顺序栈操作的实现:出栈

/*若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK；否则返回ERROR*/
Status Pop(SqStack *S, ElemType *e){
    if(S->top == -1){
        return ERROR;
    }
    *e = S->data[S->top];   //将要删除的栈顶元素赋值给e
    S->top--;   //栈顶指针减一
    return OK;
}

顺序栈操作的实现:顺序取栈顶元素

/*读栈顶元素*/
Status GetTop(SqStack S, ElemType *e){
    if(S->top == -1){   //栈空
        return ERROR;
    }
    *e = S->data[S->top];   //记录栈顶元素
    return OK;
}

top指针依旧不变

共享栈

利用栈底位置相对不变的特征，可让两个顺序栈共享一个一维数组空间，将两个栈的栈底分别设置在共享空间的两端，两个栈顶向共享空间的中间延伸

共享栈的空间结构

/*两栈共享空间结构*/
#define MAXSIZE 50  //定义栈中元素的最大个数
typedef int ElemType;   //ElemType的类型根据实际情况而定，这里假定为int
/*两栈共享空间结构*/
typedef struct{
	ElemType data[MAXSIZE];
	int top0;	//栈0栈顶指针
	int top1;	//栈1栈顶指针
}SqDoubleStack;

共享栈进栈

/*插入元素e为新的栈顶元素*/
Status Push(SqDoubleStack *S, Elemtype e, int stackNumber){
    if(S->top0+1 == S->top1){   //栈满
        return ERROR;
    }
    if(stackNumber == 0){   //栈0有元素进栈
        S->data[++S->top0] = e; //若栈0则先top0+1后给数组元素赋值
    }else if(satckNumber == 1){ //栈1有元素进栈
        S->data[--S->top1] = e; //若栈1则先top1-1后给数组元素赋值
    }
    return OK;
}

栈的链式存储

采用链式存储的栈称为链栈，链栈的优点是便于多个栈共享存储空间和提高其效率，且不存在栈满上溢的情况。通常采用单链表实现，并规定所有操作都是在单链表的表头进行的。这里规定链栈没有头节点，Lhead指向栈顶元素

对于空栈来说，链表原定义是头指针指向空，那么链栈的空其实就是top=NULL的时候。

链栈的结构代码如下：

/*栈的链式存储结构*/
/*构造节点*/
typedef struct StackNode{
    ElemType data;
    struct StackNode *next;
}StackNode, *LinkStackPrt;
/*构造链栈*/
typedef struct LinkStack{
    LinkStackPrt top;
    int count;
}LinkStack;

链栈的进栈

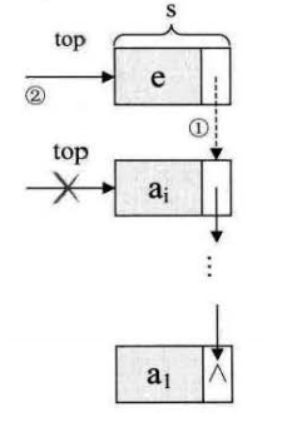
/*插入元素e为新的栈顶元素*/
Status Push(LinkStack *S, ElemType e){
    LinkStackPrt p = (LinkStackPrt)malloc(sizeof(StackNode));
    p->data = e;
    p->next = S->top;    //把当前的栈顶元素赋值给新节点的直接后继
    S->top = p; //将新的结点S赋值给栈顶指针
    S->count++;
    return OK;
}

链栈的出栈

假设变量p用来存储要删除的栈顶结点，将栈顶指针下移以为，最后释放p即可

/*若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK；否则返回ERROR*/
Status Pop(LinkStack *S, ElemType *e){
    LinkStackPtr p;
    if(StackEmpty(*S)){
        return ERROR;
    }
    *e = S->top->data;
    p = S->top; //将栈顶结点赋值给p
    S->top = S->top->next;  //使得栈顶指针下移一位，指向后一结点
    free(p);    //释放结点p
    S->count--;
    return OK;
}

性能分析

链栈的进栈push和出栈pop操作都很简单，时间复杂度均为O(1)。
对比一下顺序栈与链栈,它们在时间复杂度上是一样的,均为O(1)。对于空间性能,顺序栈需要事先确定一个固定的长度,可能会存在内存空间浪费的问题,但它的优势是存取时定位很方便,而链栈则要求每个元素都有指针域,这同时也增加了一些内存开销,但对于栈的长度无限制。所以它们的区别和线性表中讨论的一样,如果栈的使用过程中元素变化不可预料,有时很小,有时非常大,那么最好是用链栈,反之,如果它的变化在可控范围内,建议使用顺序栈会更好一些。

栈的应用——递归

在递归调用的过程中,系统为每一层的返回点、局部变量、传入实参等开辟了递归工作栈来进行数据存储,递归次数过多容易造成栈溢出等。而其效率不高的原因是递归调用过程中包含很多重复的计算。下面以n=5为例,列出递归调用执行过程,如图所示：

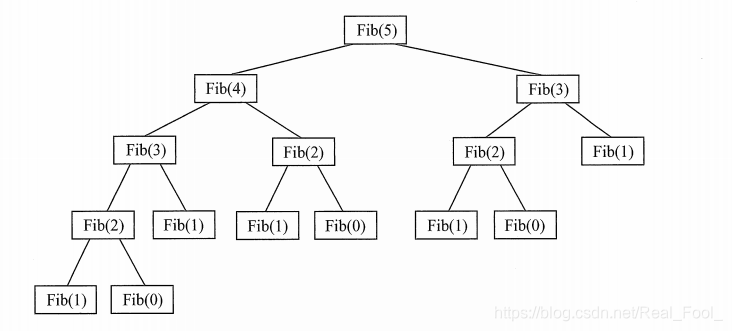
如图可知，程序每往下递归一次，就会把运算结果放到栈中保存，直到程序执行到临界条件，然后便会把保存在栈中的值按照先进后出的顺序一个个返回，最终得出结果。

栈的应用——四则运算表达式求值

1、后缀表达式计算结果

表达式求值是程序设计语言编译中一个最基本的问题,它的实现是栈应用的一个典型范例。中缀表达式不仅依赖运算符的优先级,而且还要处理括号。 后缀表达式的运算符在操作数后面，在后缀表达式中已考虑了运算符的优先级,没有括号,只有操作数和运算符 。例如中缀表达式A + B ∗ ( C − D ) − E / F所对应的后缀表达式为A B C D − ∗ + E F / − 。

后缀表达式计算规则：从左到右遍历表达式的每个数字和符号，遇到是数字就进栈，遇到是符号，就将处于栈顶两个数字出栈，进项运算，运算结果进栈，一直到最终获得结果。

将后缀表达式与原运算式对应的表达式树(用来表示算术表达式的 二元树 )的后序遍历进行比较,可以发现它们有异曲同工之妙。
如下图则是A + B ∗ ( C − D ) − E / F 对应的表达式，它的后序遍历即是表达式A B C D − ∗ + E F / −

2、中缀表达式转后缀表达式

我们把平时所用的标准四则运算表达式,即a + b − a ∗ ( ( c + d ) / e − f ) + g a+b-a((c+d)/e-f)+ga*+b−a∗**((c+d)/e−f**)**+g叫做中缀
表达式。因为所有的运算符号都在两数字的中间,现在我们的问题就是中缀到后缀的转化。

规则:从左到右遍历中缀表达式的每个数字和符号,若是数字就输出,即成为后缀表达式的一部分;若是符号,则判断其与栈顶符号的优先级,是右括号或优先级低于栈顶符号(乘除优先加减)则栈顶元素依次出栈并输出,并将当前符号进栈,一直到最终输出后缀表达式为止。

下面有一个个人的见解

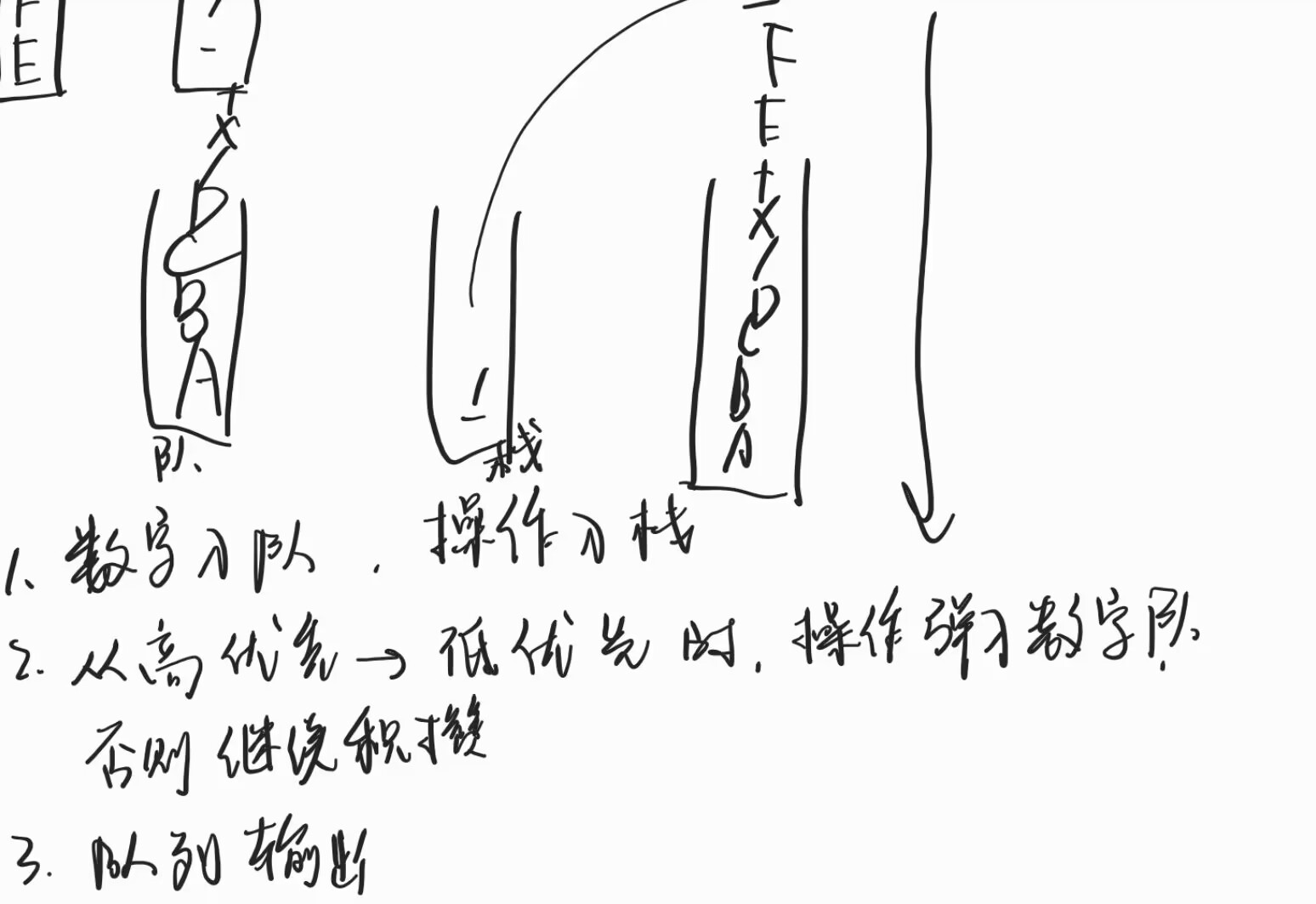
遇到括号时需记录此时符号栈指针作为括号内计算的栈底，然后重复流程

循环队列的表示与操作的实现

在循环队列的顺序存储结构中，除了用一组地址连续的存储单元依次存放从队列头到队列尾的元素之外，尚需附设两个指针 front和reár 分别指示队列头元素及队列尾元素的位置。
为了在 C/C++语言中描述方便起见，在此我们约定:初始化建空队列时，令front=rear=0,每当插入新的队列尾元素时，“尾指针增 1“;每当删除队列头元素时，“头指针增1”。因此，在非空队列中，头指针始终指向队列头元素，而尾指针始终指向队列尾元素的下一个位置，如图所示。

循环队列计算

解决假溢出的方法就是后面满了，就再从头开始，也就是头尾相接的循环。我们把队列的这种头尾相接的顺序存储结构称为循环队列。
当队首指针 Q->front = MAXSIZE-1后，再前进一个位置就自动到0，这可以利用除法取余运算（%）来实现。

初始时 ：Q->front = Q->rear=0。
队首指针进1 ：Q->front = (Q->front + 1) % MAXSIZE。
队尾指针进1 ：Q->rear = (Q->rear + 1) % MAXSIZE。
队列长度 ：(Q->rear - Q->front + MAXSIZE) % MAXSIZE。

区分满时和空时：

那么，循环队列队空和队满的判断条件是什么呢？
显然，队空的条件是 Q->front == Q->rear 。若入队元素的速度快于出队元素的速度，则队尾指针很快就会赶上队首指针，如图( d1 ）所示，此时可以看出队满时也有 Q ->front == Q -> rear 。
为了区分队空还是队满的情况，有三种处理方式：

（1）牺牲一个单元来区分队空和队满，入队时少用一个队列单元，这是种较为普遍的做法，约定以“ 队头指针在队尾指针的下一位置作为队满的标志 ”

队满条件 ： (Q->rear + 1)%Maxsize == Q->front
队空条件仍 ： Q->front == Q->rear
队列中元素的个数 ： (Q->rear - Q ->front + Maxsize)% Maxsize

（2）类型中增设表示元素个数的数据成员。这样，队空的条件为 Q->size == O ；队满的条件为 Q->size == Maxsize 。这两种情况都有 Q->front == Q->rear
（3）类型中增设tag 数据成员，以区分是队满还是队空。tag 等于0时，若因删除导致 Q->front == Q->rear ，则为队空；tag 等于 1 时，若因插入导致 Q ->front == Q->rear ，则为队满。

循环队列操作的实现:定义存储结构

//-----循环队列---队列的顺序存储结构
#deEime MAXQSIZE 100
//最大队列长度
typedef struct {
    QrlemType *base;        //初始化的动态分配存储空间
    int front;              //头指针,若队列不空,指向队列头元素  
    int rear ;              //尾指针,若队列不空,指向队列尾元素的下一个位置

}SqQueue;

循环队列操作的实现:求长度

int QueueLength(SqQueue Q){
    //返回Q的元素个数,即队列的长度
    return(Q.rear-Q.front+MAXOSIZE)% MAXQSIZE;
}

循环队列操作的实现:插入新元素

Status EnQueue(SqQueue &Q,QrlemType e){
    //在队列Q的尾部插入元素e
    if((Q.rear+1)%MAXQSIZE == Q.front){
        //队列满,追加存储空间
        Q.base=(QrlemType *)realloc(Q.base,(Q.stacksize + QUEUEINCREMENT)*sizeof(QrlemType));
        if(!Q.base)exit(OVERFLOW); //存储分配失败
        Q.stacksize += QUEUEINCREMENT;
    }
    Q.base[Q.rear] = e;
    Q.rear = (Q.rear+1)%MAXQSIZE;
    return OK;
}

循环队列操作的实现:删除元素

Status DeQueue(SqQueue &Q,QrlemType &e){
    //删除队列Q的头部元素,并用e返回其值
    if(Q.front == Q.rear){
        //队列空
        return ERROR;
    }
    e = Q.base[Q.front];
    Q.front = (Q.front+1)%MAXQSIZE;
    return OK;
}

双端队列

1、定义

双端队列是指允许两端都可以进行入队和出队操作的队列 ，如下图所示。其元素的逻辑结构仍是线性结构。将队列的两端分别称为前端和后端，两端都可以入队和出队。

在双端队列进队时，前端进的元素排列在队列中后端进的元素的前面，后端进的元素排列在队列中前端进的元素的后面。在双端队列出队时，无论是前端还是后端出队，先出的元素排列在后出的元素的前面。

总结

栈是限定仅在表尾进行插入或删除的线性表，又称为后进先出的线性表。栈有两种存储表示，顺序表示(顺序栈)和链式表示(链栈)。栈的主要操作是进栈和出栈，对于顺序栈的进栈和出栈操作要注意判断栈满或栈空。
队列是一种先进先出的线性表。它只允许在表的一端进行插入，而在另一端删除元素。队列也有两种存储表示，顺序表示(循环队列)和链式表示(链队)
栈和队列的逻辑结构都和线性表一样，数据元素之间存在一对一的关系。

循环队列中少用一个元素判断队空或队满时:
队空的条件: Q.front == Q.rear
队满的条件: (Q.rear+1)%MAXQSIZE == Q.front